
Logaritmo neperiano, nepe… qué, neperiano. Ahí te quedas!

No, no os vayáis, aguantad, por favor. Tanto vosotros como yo odiamos los logaritmos, pero a los enemigos es mejor conocerlos y saber por dónde pueden salir. En este artículo voy a intentar ayudaros a que conozcáis mejor estos entes matemáticos que tanta animadversión despiertan. De todos modos, como siempre le digo a mis alumnos, hay dos tipos de personas en este mundo, los que conocen los logaritmos y los que no. Y no me digáis que no os gustaría entrar en un garito y cuando abráis la puerta, aquellos que se encuentren dentro digan para sí: “esta o este tiene una cara de controlar los logaritmos… son seres superiores”. Os lo aseguro, que eso se nota solo con un golpe de vista.
Vamos a ello, pero despacito, para que nadie se nos quede atrás.
Una potencia es la multiplicación de un número por sí mismo un número determinado de veces.
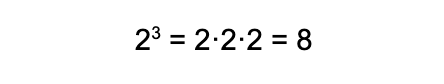
Al número 2 se le llama base y al 3 exponente. ¿Hasta aquí todo bien, verdad?
Ahora poned los cinco sentidos:

Como 2·2·2 = 8, hemos tenido que multiplicar el número 2 tres veces por sí mismo para que nos dé 8, entonces:
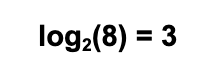
Veamos un par de ejemplos más:

En definitiva un logaritmo es el exponente al que hay que elevar la base para que nos dé el argumento.
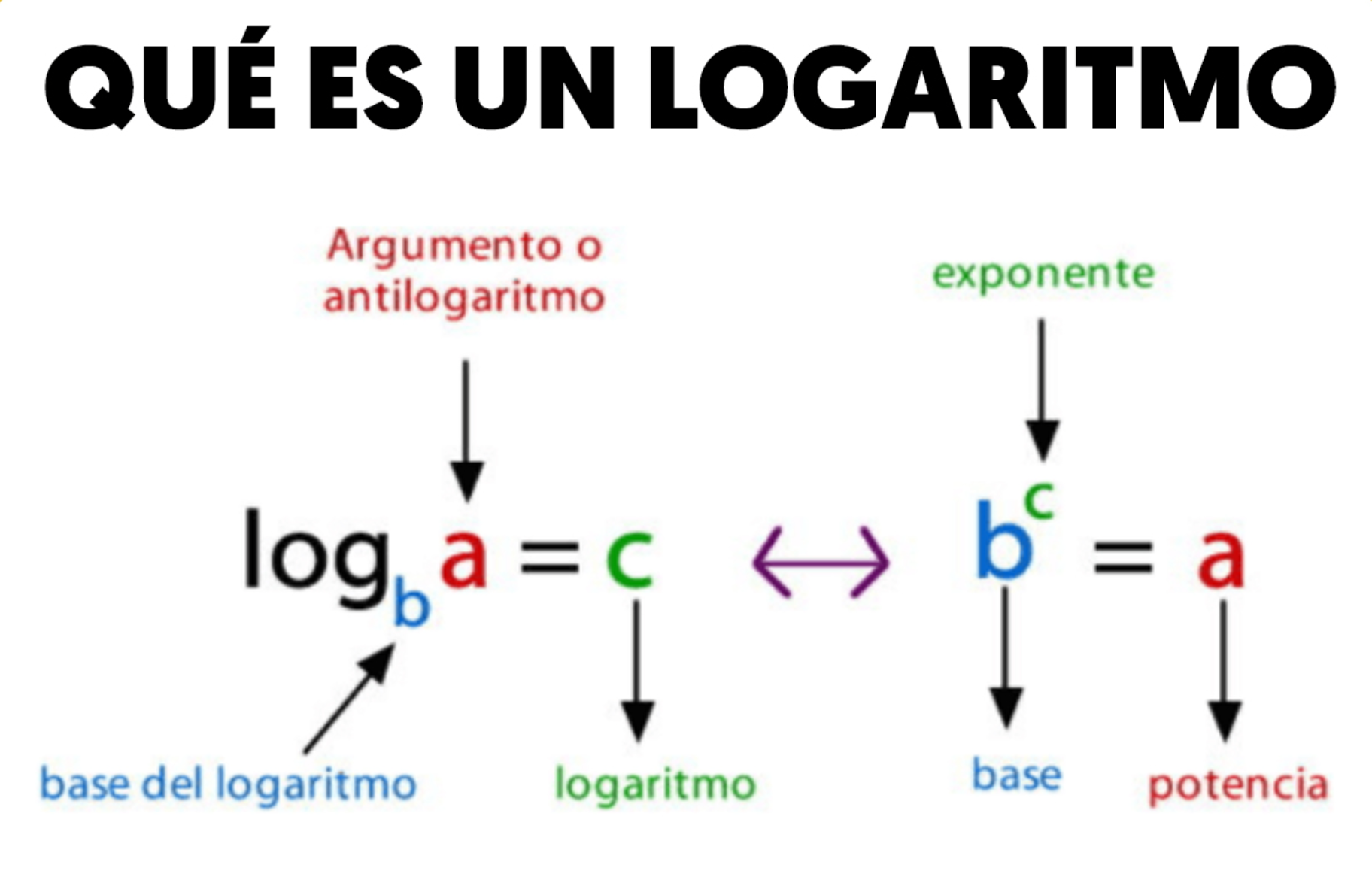
Pues ya está, se acabó, esto es todo lo que hay que saber, ya sois expertos en logaritmos.
Dicho esto, la pregunta que siempre nos hacemos. Y para qué, qué función tienen los logaritmos en esta vida… La principal misión es la de “suavizar” las subidas o las caídas. Si algo crece rápidamente y le aplicamos un logaritmo, esa subida la sigue haciendo, pero de forma mucho más suave. Vamos a verlo:

Si os fijáis la sucesión 4, 8, 16, 32, 64, 128, 256, tiene un crecimiento muy rápido (crecimiento exponencial). En cambio si le aplicamos un logaritmo, en este caso, en base 2, se convierte en la sucesión 2, 3, 4, 5, 6, 7, 8,… que va creciendo de uno en uno (crecimiento lineal), mucho más suave, como decíamos. Para que lo entendáis con un caso real, si Elon Musk le aplico un buen logaritmo, lo dejo con mi sueldo ;).
Dentro de los logaritmos, como en todo, siempre hay unos más especiales que otros.
Los dos más famosos son el logaritmo en base 10, que se escribe simplemente log y el logaritmo neperiano que lo denotamos por ln y es el logaritmo en base e = 2,718281…, un número irracional como Pi.
Lo de neperiano viene del matemático escocés Jonh Napier, el primero en publicar, en 1614, métodos de cálculo mediante logaritmos. Pero, como estaréis comprobando en esta serie de publicaciones matematicofóbicas, nunca hay un descubridor claro. Cuatro años antes de esta publicación, Joost Bürgi, un matemático y relojero suizo los descubrió, pero no fue hasta 1618 cuando los sacó a la luz y para entonces Napier ya se le había adelantado. ¿Llegó el descubrimiento de Bürgi a las manos de Napier? No sabemos pero lo cierto es que el que pega primero, pega dos veces.
Aunque lo verdaderamente interesante de los logaritmos es su aplicación a las diferentes áreas del conocimiento.
Una de las más significativas es su papel en el cálculo de la antigüedad de un fósil mediante el estudio del Carbono- 14 (C14). En cuanto los organismos vegetales o animales mueren, el porcentaje de C-14 de la materia orgánica muerta comienza a disminuir y lo hacen a un ritmo exponencial que es conocido. De la misma forma que subía 4,8,16,32,… éste, a lo largo de los años, baja. Con la ayuda de los logaritmos podemos calcular la antigüedad de dichos fósiles. Imaginaos lo que supone esto en el estudio de la historia de la humanidad.
Otro de los campos más conocidos donde se aplican es en la medición de la intensidad de los terremotos, la famosa escala Richter. Cuando escuchamos que ha habido un terremoto en Japón de intensidad 6 grados, es una medición en escala logarítmica y aquí es donde vamos a intentar entender en qué consiste.
La escala Richter se mide en logaritmo en base 10, lo que significa que un terremoto de 7 grados tiene una intensidad diez veces mayor que uno de 6 y cien veces más que uno de intensidad 5. Por lo que ya podéis haceros una idea de la fuerza del maremoto de 9,1 grados que azotó en aguas de Kaluntara (Sri Lanka) en 2004 provocando el peor tsunami de la historia moderna, llegando en tan solo dos horas, a las costas de Indonesia, Tailandia y Myanmar donde se vieron invadidos por olas de más de 30 metros de altura. El resultado de la tragedia se saldó con casi 300.000 muertos.
Otras de las aplicaciones logarítmicas son la medición del brillo de las estrellas o los niveles de pH en la piel, el agua o en los alimentos.
Y con esto yo creo que ya podéis pavonearos por los bares, restaurantes y chiringuitos del mundo con esa cara de dominar los logaritmos que estáis echando, si es que os lo noto desde aquí.
¡Hasta la semana que viene loguitos!























