
Lo mismo tienes un fractal al lado y no lo sabes

Hasta bien entrado el siglo XX se habían intentado estudiar los objetos y formas que nos rodean en nuestro día a día aplicando la geometría tradicional, pero de poco valen estas técnicas para estudiar algunos fenómenos de la naturaleza. Decía Benoit Mandelbrot en la introducción a su libro «Geometría Fractal de la Naturaleza»: “Las nubes no son esferas, las montañas no son conos, las costas no son círculos, y las cortezas de los árboles no son lisas, ni los relámpagos viajan en una línea recta” .
Intentar modelizar estos y otros fenómenos naturales y científicos dio pie a Mandelbrot a poner en la mesa de las matemáticas un nuevo plato, cocina fusión. Lo hizo con el artículo “¿Cuánto mide la costa de Gran Bretaña?, publicado en la revista Science, en el año 1967, hace dos días. En él venía a decir que la longitud de la costa será mayor, cuanto menor sea la unidad de medida que usemos, buscando patrones en la rugosidad, grietas o fracturas que nos encontramos en la naturaleza o en fenómenos aparentemente caóticos. De ahí viene el nombre de fractal (del latín fractus: quebrado, fracturado), que este autor acuñó en 1975.
Pero diréis, ¿qué carajo es un fractal? Aquí viene lo mejor, aún, a día de hoy no hay una definición rigurosa de este concepto. ¿Qué os pasa matemáticos y matemáticas del mundo? ¿No dais con la tecla?
Así que nos tendremos que acercar a dicho concepto de una forma intuitiva para que nos dé una idea de los que son.
Lo mejor es construir uno y a partir de él trabajarlo. ¿Os parece bien? Y si no, mala suerte, porque lo voy a hacer así. Al lío.
Construyamos el copo de nieve de Koch, también llamado estrella de Koch. Su construcción se realiza mediante un proceso iterativo que se inicia con un triángulo equilátero. Cada lado lo dividimos en tres partes iguales, tomamos como referencia la parte central y con esa longitud construimos otro triángulo equilátero, finalmente eliminamos el segmento que habíamos tomado de referencia. Y así lo vamos haciendo con cada uno de los segmentos que nos va quedando. Os dejo la construcción para que lo veáis claro.
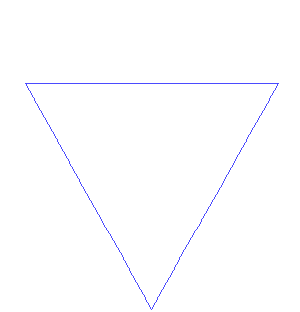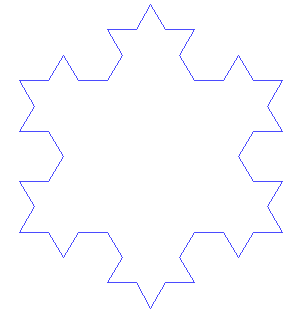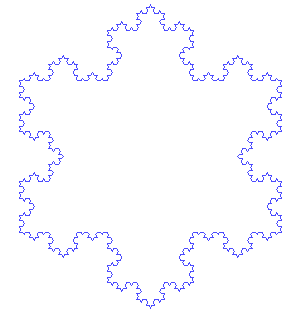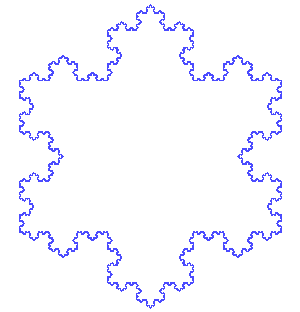
Esta estrella es un ejemplo de una curva cerrada continua pero no derivable en ningún punto. Fue descrita por el matemático sueco Helge von Koch en 1904, como ejemplo de curvas continua no derivable. Fijaos, anterior a Mandelbrot.
Después de este ejemplo, podríamos acercarnos al concepto de fractal como aquellos objetos o formas cuya estructura se repite a diferentes escalas, es decir, tienen la propiedad de la autosimilitud. Entendiendo como figura geométrica autosímil aquella que al hacer zoom sobre una de sus partes reconocemos la forma de toda la figura.
Veamos otro ejemplo, este en el plano.
Como del triángulo ya os hablé en el artículo Los secretos del triángulo de Pascal, os voy a presentar la alfombra de Sierpinski, que partiendo de un cuadrado, dividimos sus lados en tres partes iguales y trazando paralelas por esas particiones nos queda dividido en nueve cuadrados iguales. Quitamos el central y con los ocho restantes volvemos a repetir el proceso iterativamente. Nos queda la siguiente figura:

Aunque existen fractales que no tienen autosimilitud y esto crea un problema en la aproximación de definición que habíamos dado, así que se ha virado hacia el uso del concepto de dimensión.
Pongamos un ejemplo, una línea recta decimos que tiene dimensión 1 y un plano tiene dimensión 2; pero la «estrella de Koch» podemos comprobar que estar a camino entre una línea y un área. Podríamos decir que los fractales son “más que líneas” pero “menos que áreas”, o “más que puntos” pero “menos que líneas”. Por eso se dice que su dimensión es fraccionaria o no entera.
No voy a entrar en la definición de dimensión de un fractal, simplemente diré que se utilizan diferentes cálculos de ellas ya sean objetos con autosimilitud (dimensión D) u objetos fractales no tan regulares en los que que se utiliza la dimensión de Hausdorff.
Pero lo sorprendente de los fractales está en la cantidad de elementos que nos rodean donde podemos encontrarlos y seguro que lo desconocemos.
Abrid Google Earth y colocaos sobre la cuenca del Tajo. ¿Qué veis? Afluentes a la derecha y a la izquierda. Si nos acercamos a uno de ellos, por ejemplo el río Alagón, afluente por la derecha… ¿Qué apreciáis? Que le vuelve a llegar agua de otros ríos y arroyos más pequeños, le entra por la derecha y por la izquierda, volved a hacer zoom y fijaos en uno de los afluentes de este último, uno de los más importantes… el río Jerte, que baja desde el valle que lleva su nombre, ¿qué encontráis a ambos lados? La llegada de agua procedente de regatos, arroyos, riveras… Ahí tenéis un fractal. Maravilloso, ¿verdad?
En el brócoli romanesco podemos distinguir perfectamente una estructura fractal, donde el patrón se repite una y otra vez a diferentes escalas.

Uno de los ejemplos más bellos son los copos de nieve con estructuras hexagonales que se repiten de forma continuada tanto si observamos sus cristales individuales, como si nos centramos en las formaciones más grandes.

En los helechos se puede apreciar la autosimilitud: una hojita que sale del tallo tiene la forma de un helecho completo, sólo que su tamaño es menor.

Pero no me quiero despedir sin mostraros el que dicen que es el fractal más bello del mundo, que lleva su nombre en honor al padre de esta geometría, Mandelbrot.
Este conjunto se define en el plano complejo fijando un número complejo c cualquiera. A partir de c, se construye una sucesión por recursión:

Si esta sucesión queda acotada, entonces se dice que c pertenece al conjunto de Mandelbrot, y si no, queda excluido y la forma que toma es:

También son famosos en el plano complejo los fractales denominados conjuntos de Julia, así llamados por el matemático Gaston Julia.
Podríamos seguir con ejemplos como cadenas montañosas, líneas de costas o su aplicación al arte, a la música o la ciencia de datos, cómo no.
En fin, tiene trabajo por delante el mundo matemático en este campo… principalmente, a ver si dan con la definición, que ya les vale.
Salud y sed felices.
























