El principio del palomar

Aquellos de vosotros que estéis inmersos en estos escritos de El hater, habréis comprobado que mucho cariño no le tengo al afán que tienen las matemáticas de complicarlo todo. Hoy os traigo un caso peculiar, si algo es sencillo, como es ésto, por qué hay que retorcerlo y retorcerlo hasta la saciedad. 

No sé si conocéis el principio del palomar, dice algo tan obvio como que si existen 9 palomares y en él se albergan por la noche para descansar 10 palomas, al menos, en uno de los palomares tienen que dormir 2 de ellas. 

De forma genérica este principio dice: Si existen más palomas que palomares,  en alguno de los palomares tiene que haber por lo menos dos palomas. 

Es algo que se cae por su propio peso y nadie puede poner en duda. Estupendo, un razonamiento lógico, sencillo, incluso si cerramos los ojos podemos ver a las palomitas dormidas por la noche cada una en su sitio… 

Pero en el mundo matemático hay que buscarle los tres pies al gato, estirar el chicle que si no, no se quedan tranquilos y entonces llega un día uno de ellos y dice: 

Aplicando este principio, en una fiesta, siempre hay al menos dos personas que tienen el mismo número de conocidos. ¿Cómo…?

Sí señores y señoras, esto es así. Imaginemos, para traerlo a nuestro terreno que os invito a una fiesta en mi casa y en total somos 16 personas. Si os he invitado todos, al menos, me conocéis a mí, por lo que todo el mundo conoce, por lo menos a una persona. ¿Qué puede pasar? Que cada uno de los que estamos conoce de 1 a 15 personas. El número de personas conocidas van a ser los palomares, los vamos a numerar del 1 al 15. Y las personas que asisten a la fiesta somos las palomas, que en total hay 16. Como hay más palomas que palomares, por el principio anterior, por lo menos dos personas van a coincidir en el número conocidos. ¿Cómo os quedáis? 

Apretemos un poco más ¿Sabéis que es La Quema de Torrejoncillo? Para el que la desconozca, es un espectáculo teatral que se celebra el segundo fin de semana de julio en mi pueblo y al que tenéis que venir porque es de las cosas que hay que ver en vida, el Louvre y La Quema. Ésta se celebra en la plaza y tiene un aforo de unas 2000 personas. 

Por el principio del palomar podemos asegurar que en cualquiera de las representaciones al menos hay dos personas que coinciden en la inicial de su nombre de pila (si tiene dos, el primero) y en la primera letra de su primer apellido. Un caso sería, por ejemplo, Cristina Montero y Cristofer Moreno. 

Vamos a la demostración. Para esquematizarlo, si una persona se llama Dolores Romero lo representaremos por (d,r) y a Pedro Rodrigo por (p,r). El primer paso que vamos a dar es calcular cuántas formas hay de que una persona tenga iniciales del nombre y primer apellido distintos. El abecedario español está formado por 27 letras desde el año 2010 según la RAE, así: 

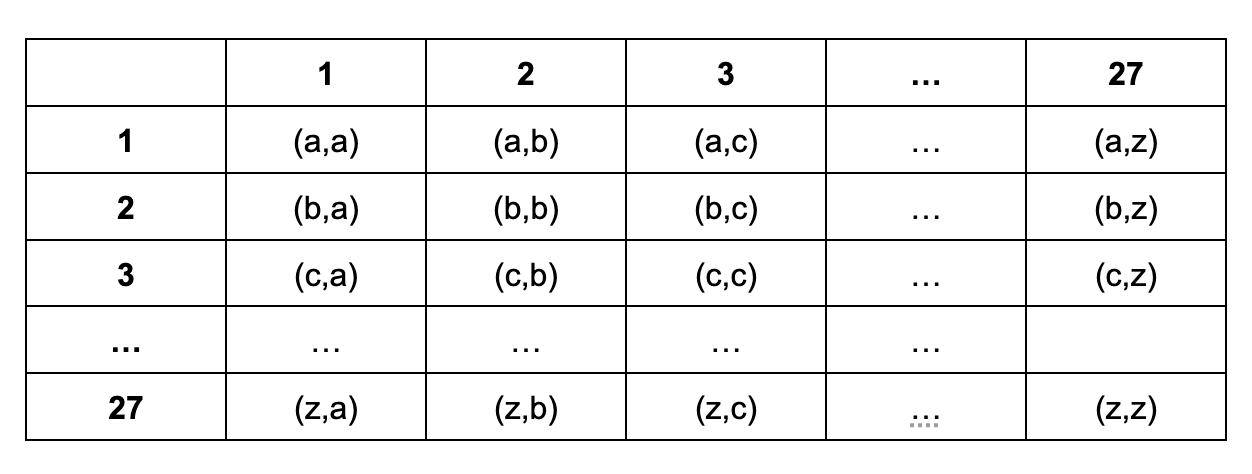Según este cuadro, se puede comprobar que son 27 x 27 = 729 formas de que una persona tenga la inicial de su nombre y la primera letra de su primer apellido diferentes. Estos van a ser nuestros palmares. Ahora, cada persona que asiste a la obra de La Quema (nuestras palomas) tendrá un nombre y un primer apellido, por lo tanto lo metemos en uno de nuestros palomares de dos letras. Como son 2000 personas (palomas), en alguno de los palmares tendrá que haber por lo menos dos de ellas, que en este caso se traduce en que coinciden la inicial de su nombre y de su primer apellido. Como queríamos demostrar (c.q.d.)   

Existen otros enunciados clásicos de este principio como: En Guatemala al menos hay dos personas con el mismo número de pelos en la cabeza o en un colegio con 400 alumnos, al menos hay dos que cumplen años el mismo día. 

En el primero, se estima que la cabeza (bien poblada) de una persona puede tener en torno a 150.000 cabellos (palomares), pero la población de Guatemala supera el millón de habitantes (palomas). En el segundo ejemplo, los días del año son como mucho 366, si el año es bisiesto, nuestros palomares y los niños del cole, las palomas. 

Yo creo que ya le váis pillando el truquillo, ¿verdad? 

El principio del palomar también recibe el nombre del principio de las cajas, de las casillas o de Dirichlet, en honor al matemático alemán Johann Peter Gustav Lejeune Dirichlet debido al tratado que escribió sobre el principio en 1834 con el nombre de Schubfachprinzip («principio de los cajones»).

Pero no quedaron tranquilos con ello, que han seguido dándole vueltas y existe una versión generalizada del principio del palomar, que viene a decirnos que si hay muchas más palomas que palomares, por ejemplo, si las palomas son el número de personas que fueron al concierto de Manuel Carrasco al estadio de la Cartuja en Sevilla en 2022, que es el récord de asistencia a un concierto en España con 74.345 personas. Y los palomares el día de su cumple, que hay 366 días como máximo. No sólo podemos decir que al menos hay dos personas que cumplen años el mismo día, sino que al menos hay 204 personas que los cumplen el mismo día, que sale de dividir el número de asistentes entre el número días del año (74.345 : 366 = 203,12).

A pesar de su aparente sencillez, este dichoso principio es una potente herramienta dentro de la combinatoria, con aplicaciones en campos como la teoría de grafos, el análisis matemático, la geometría, la teoría de números o la computación.

Y no sigo porque esto va a peor… Qué forma de complicarlo todo, me piro… ¡Montoya va donde brilla… salta la gamba, salta la gamba!