El número de oro (I)

Supongo que no lo sabéis, pero este es el vigésimo quinto artículo de El hater matemático y por ser un número especial, lo vamos a celebrar escribiendo sobre otro número aún más especial en matemáticas, a la altura de π, me atrevería a decir. El número áureo, también llamado número de oro, proporción áurea, divina proporción o razón dorada… entre muchas otras. 

Pero antes de entrar en materia me gustaría que cogieseis lápiz, papel, regla y calculadora, venga buscadla, y hagáis un prueba muy sencilla. Trazad un segmento y dividirlo en dos partes que no sean iguales, una mayor que la otra, como os apetezca. Ahora haced tres mediciones, el segmento inicial y las dos partes en las que lo habéis dividido. Seguidamente haced dos divisiones: en primer lugar la longitud del segmento original entre su parte más larga y después dividid la parte más larga entre la corta. ¿Os han salido números parecidos? 

Os voy a proponer otro juego relacionado con el anterior. Ahora quiero que dibujéis un rectángulo que no sea cuadrado, es decir, que la base sea más larga que la altura, o viceversa, da igual. El que os parezca, a vuestro entender, que es más agradable a vista. Medid la base y la altura y dividid el lado más largo entre el más corto. ¿Qué cantidad os sale? ¿Se parece a las dos anteriores? ¿Os ha salido algo cercano a 1,6?

Estas dos pruebas sería interesante que las hicieseis antes de seguir leyendo, si no lo hacéis, no pasa nada, cuando acabéis de leer el artículo estoy seguro que lo haréis. El ser humano es así de cotilla. Luego enganchamos con esto. 

Vamos a lo que nos compete hoy. El número de oro se representa por la letra griega φ (phi) (en minúscula) o Φ (Phi) (en mayúscula) en honor al escultor griego Fidias y es un número irracional y algebraico con un valor aproximado a 1,618033988749894… – recordemos que un número irracional es aquel no se puede poner como cociente de dos números enteros, tiene infinitos decimales de forma no periódica y algebraicos son aquellos números que son soluciones de una ecuación con coeficientes racionales– concretamente esta: 

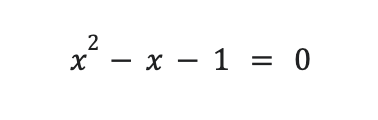
Vamos a resolver esta ecuación de segundo grado a ver qué sale: 

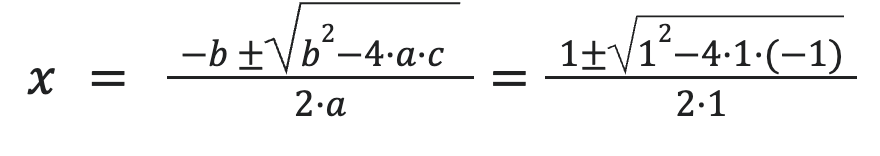
Nos da dos soluciones 

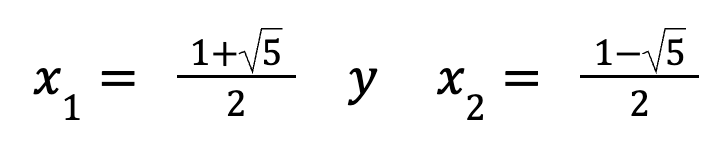
Ahí lo tenemos, una de las dos soluciones es nuestro número

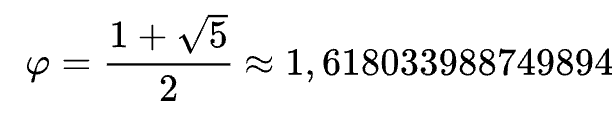
Hasta aquí nada nuevo, ya que raíz(5) es un número irracional, si le sumamos 1 y después lo dividimos por dos, sigue siendo irracional. Además, este tipo de números no es difícil encontrar una ecuación de la que sean solución para que verifique la condición de algebraico. En fin, a mí no me parece nada especial, pero el mundo matemático se ha vuelto loco con este numerito… Creo que se han dado un cúmulo de casualidades en torno al mismo que algunos le han visto cualidades divinas, de ahí sus nombres, pero ya sabéis cómo se las gasta este colectivo…

Veamos algunas de sus propiedades aritméticas:

• Una de las más curiosas es que φ ≈ 1,618033988749894… y su inverso (1/φ ≈ 0,618033988749894…) tienen las mismas infinitas cifras decimales.

• Si a φ le sumas 1 nos da su cuadrado. 

• Si a φ le restas 1 nos da su inverso. 

• Si al cuadrado de φ le restas su inverso el resultado es 2. 

• El cubo de φ sale como resultado de dividir φ + 1 entre  φ – 1  

• Además cualquier potencia de φ es la suma de φ elevado a uno menos y φ elevado a dos menos. 

Pero todo esto, salvo la primera, que es pura chorra, se desprende de que φ es solución de la ecuación que os presentaba al principio.  

Además fruto de esta relación también se puede expresar como una fracción continua: 

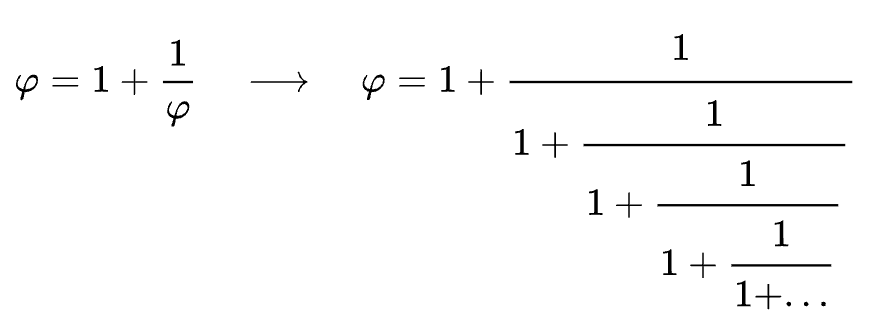
O raíces anidadas:

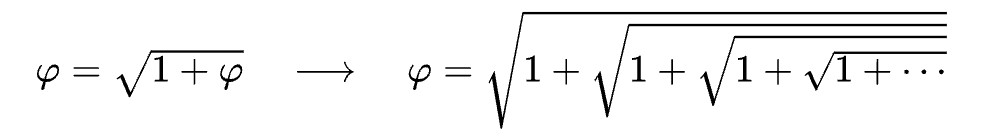
Por ahora todo sale del mismo sitio prácticamente, aunque han encontrado alguna cosilla más. Resulta que también se puede expresar como expresión trigonométrica

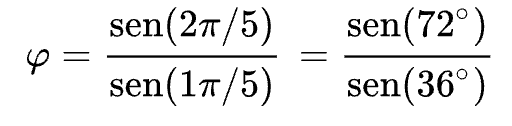
O como el límite de la división entre dos elementos consecutivos de la sucesión de Fibonacci. 

Recordemos, definimos la sucesión de Fibonacci del siguiente modo:

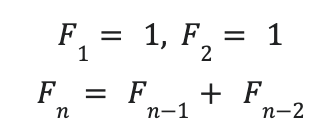
De esta manera.

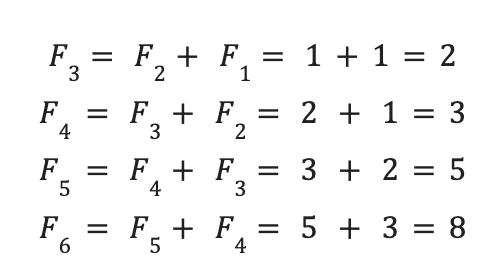
Aquí os dejo enlace al artículo de el hater Fibonacci y sus conejos que está íntimamente ligado con este. Pues resulta que casualmente esta sucesión se relaciona con el número de oro del siguiente modo: 

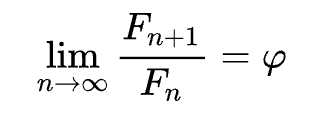
Vamos a verlo. 

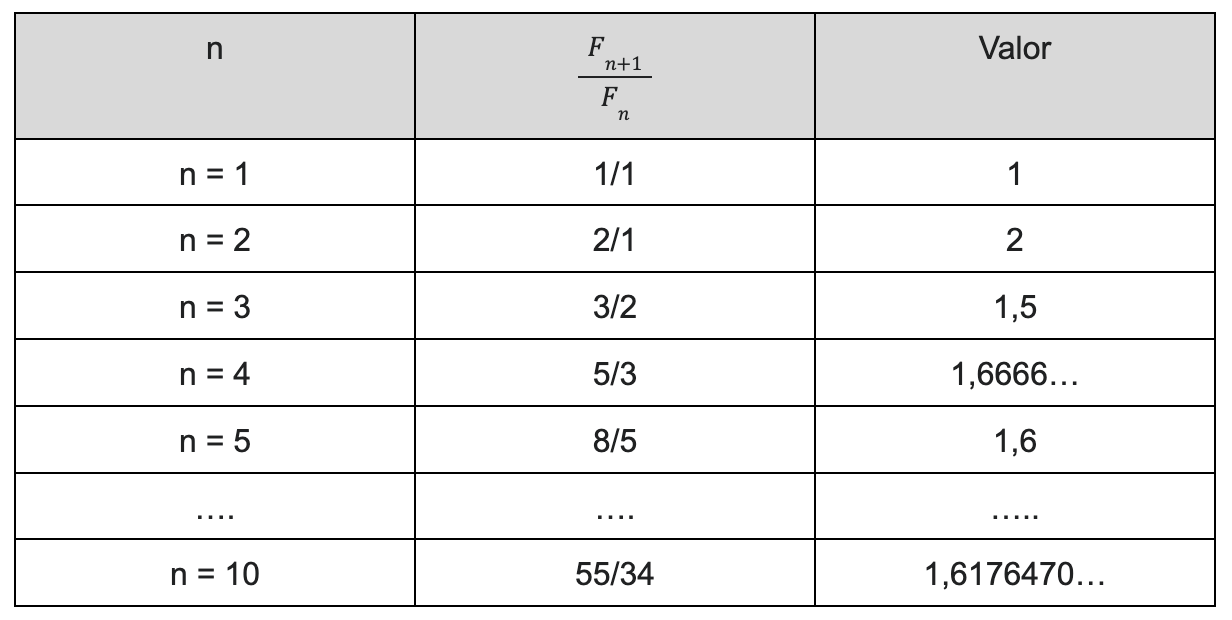
Parece ser que sí, que cada vez se acerca más… 

Estas casualidades han hecho que el mundo matemático investigara, no fuese que este número tuviese algo de especial. 

Aunque algunos autores han querido datar la aparición del número áureo en épocas babilónicas y asirias, en torno al 2000 a.C., al igual que se le ha querido asignar a Platón ( 428-347 a. C.)  su conocimiento, no hay constancia fehaciente de ello y sí que existe documentación que corrobora que fue Euclides (325 a. C – 265 a. C.) el primero en hacer un estudio formal del número áureo en el Libro 6º de Los Elementos, donde lo define. 

Ya en la Edad Moderna, 1509, el matemático y teólogo italiano Luca Pacioli publicó De Divina Proportione (La Divina Proporción), donde plantea cinco razones por las que estima apropiado considerar divino al número áureo en semejanza con la divinidad de Dios. Hasta este extremo llegaba la cosa. 

Y como esto veo que se alarga, lo vamos a dividir en dos artículos, por ahora nos hemos centrado en la parte aritmética, el número en sí, pero queda que os cuente su origen geométrico, eso del segmento o el rectángulo que os proponía al principio. Os dejo una semana para que lo hagáis y volvemos con el dichoso numerito la semana que viene y sus sorprendentes aplicaciones en la naturaleza, el arte o nuestro día a día. Eso dicen los matemáticos, ya veréis que todo es pura potra. 

Poneos a la sombra, tomad mucha agua y sed buenos.