El primo encriptado

Me gustaría poneros sobre aviso, no os fiéis ni un pelo de los números primos, son traicioneros, esquivos, huidizos… Están por todos lados, pero nunca sabes por dónde te van a salir. 

Que qué son números primos, perdón, os los presento:

Situémonos, hoy trabajaremos con los números enteros positivos, ya sabéis, sin decimales. El 1, 2, 3, 4…. hasta el infinito y más allá. 

Diremos que un número es primo si sólo tiene dos divisores, el 1 y él mismo. 

Por ejemplo, el 7 es primo porque sus únicos divisores son el 1 y el 7, si lo dividimos por cualquier otro número más pequeño que él, el resto de la división es distinto de cero. En cambio el 6 no es primo porque tiene como divisores el 1, el 2, el 3 y él mismo, el 6. A estos números se les llama compuestos. 

Por cierto, el 1 no es primo y fin de este debate.

Puestos en la casilla de salida, por qué les tengo tanta tirria a estos números, pues porque son incontrolables. Echemos un vistazo a los primeros: 2, 3, 5, 7, 11,13,17,19, 23, 29… ¿Encontráis alguna relación entre ellos? Buscadla, buscadla… La diferencia entre 2 y 3 es 1, entre 3 y 5 es 2, entre 5 y 7 vuelve a ser 2, entre 7 y 11 es 4 y podríamos seguir y seguir…. No hay un patrón que nos permita generarlos. Lo mismo se alejan que se acercan, de pronto cuando parece que han desaparecido, se presenta uno de ellos de la nada. Ingobernables, como C. Tangana.

La aparición de los primeros números primos se cree que data de hace más de 20.000 años (antes de la aparición de la escritura) en el hueso de Ishango, el cual presenta 11,13,17 y 19 hendiduras aisladas. Algunos arqueólogos interpretan con ello el conocimiento de los números primos. Pero desde luego es Euclides en su libro, Los Elementos (al que habrá que dedicarle algún artículillo) el que ya los define y además demuestra que hay infinitos. 

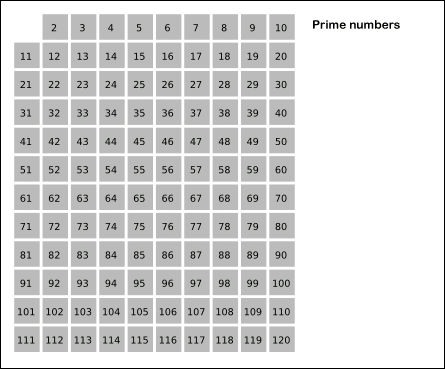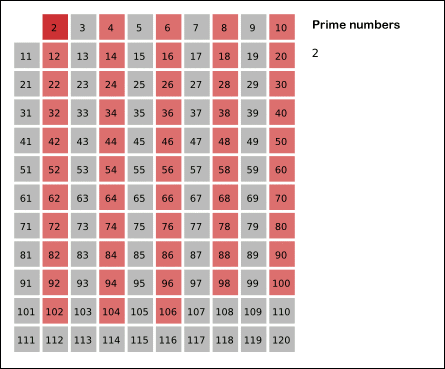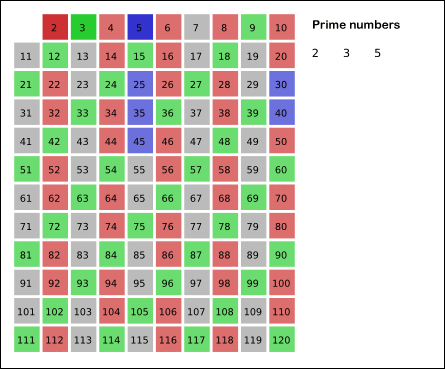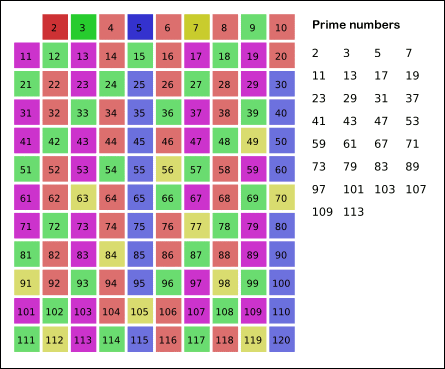
Ya sabéis, a los matemáticos les dicen infinito y se vuelven locos… Qué es lo que hacen, ponerse a buscar números primos como si no hubiera un mañana. El método más conocido, pero no el más eficiente, es la criba de Eratóstenes, que utiliza un procedimiento muy sencillo. Comienza con el primer primo, el 2 y tacha todos los múltiplos suyos menos él, ya que tienen al 2 como divisor, que junto al 1 y ellos mismos, ya tendrían al menos 3 divisiones, por lo que no pueden ser primos.  Del mismo modo hace con los múltiplos de 3, los múltiplos del 5, del 7, etc.

Pero a lo largo de la historia, han sido muchos los que han intentado buscar fórmulas para generar números primos y los cabrones, no se dejan.

Os pongo un par de ejemplos: 

Pues no tranquilos con eso, llega el Teorema Fundamental de la Aritmética que dice que todo número natural es una multiplicación única de números primos, salvo el orden. 

O sea, que sea cual sea el número que elijamos, dependemos de ellos: 

• 6 = 2·3

• 8 = 2·2·2

• 21 = 3·7

• 10.000 = 2·2·2·2·5·5·5·5

Dios, estamos en sus manos, es como cuando te enteras que ese que te cae tan mal en el trabajo, es el que va a tomar la decisión de la subida de tu sueldo. 

¿Y esta paranoia de buscar números primos tiene sentido? Por desgracia sí, esto no es como los decimales de Pi, aquí cuanto más conozcamos, mejor. 

En estos momentos hay dos campos predominantes en el mundo de la computación, la Inteligencia Artificial, que vive de los datos y la Ciberseguridad, en la búsqueda continua del traspaso de información sin que sea interceptada por terceros.

Es en este segundo campo donde juegan un papel fundamental los números primos, concretamente en la encriptación de los mensajes.

La codificación de los mensajes existe, al menos, desde la época romana. Cuando la cohorte de una legión le quería indicar a otra que atacarían el día siguiente a las siete de la mañana, el mensaje que portaba el soldado encargado de transmitir la noticia decía “al emperador le pica el segundo dedo del pie izquierdo”, ya que si era el de la mano, el ataque sería por la tarde. Eso lo sabemos todos. 

Esto es lo que se llama codificación simétrica, tanto el emisor como el receptor deben conocer la clave para desencriptar el mensaje. 

Vamos a proceder a realizar una codificación simétrica más seria, pero sencilla. 

El emisor crea una clave, por ejemplo: SARA. 

Establecemos un sistema para transformar la clave en número. Podría ser que a cada letra le asignamos su posición en el abecedario. A = 01, B = 02, C = 3… En nuestro caso S = 20, A = 01,  R = 19. De esta manera S A R A = 20 01 19 01. Ahora se elige la llave que abre y que cierra. Ésta debe ser conocida tanto por el emisor como por el receptor. 

Por ejemplo sumarle uno a cada posición: 20 +1 = 21, 01 + 1 = 02 y 19 + 1 = 20 

De esta manera la clave encriptada pasa a ser: 21 02 20 02. Finalmente, juntamos las cifras y lo enviamos: 21022002 (código que viaja y puede ser interceptado).

Cuando llega a su destino hay que descodificarlo realizando la operación inversa. Primero separamos las cifras de dos en dos: 21 02 20 02. Si antes sumamos, ahora toca restar: 21 – 1 = 20, 02 – 1 = 01 = 1 y 20 – 1 = 19. Y finalmente los números 20 01 19 01 los transformamos en letras: S A R A. 

¡Contraseña correcta, podemos entrar en instagram!

No os emocionéis, porque esto es una mierda de encriptación, un hacker de primero de infantil os la pilla en 10 segundos. 

El problema que tiene este sistema es cómo hacer llegar la llave al destinatario. 

Entonces, ¿qué pasa si creamos una encriptación con doble llave, una solo para cerrar y otra para abrir? Esto es lo que se llama codificación asimétrica y donde entran a jugar los números primos. Tachán!!!!

El algoritmo más famoso y más utilizado recibe el nombre de RSA que elimina el intercambio de claves. 

Este sistema tiene una clave privada que solo posee el receptor y una clave pública, que el receptor facilita al emisor y que puede que alguien la pille, pero no nos importa mucho.

El algoritmo no es tan sencillo como el anterior, pero a grandes rasgos se basa en que una parte de la clave privada es un número n,  que es el resultado de la multiplicación de dos números primos p y q. Y deducir cuánto valen p y q conociendo solamente n no es tarea sencilla ni para los ordenadores actuales más potentes, sobre todo cuando p y q son números primos de 100 dígitos.

Por eso nos interesa conocer números primos cuanto mayores, mejor. 

Pero parece ser que el chollo de la encriptación está en peligro con la llegada de los ordenadores cuánticos, máquinas que operan a una velocidad exponencialmente más rápida de lo que se ha hecho hasta ahora y por lo tanto, predecir los números primos p y q anteriores parece ser que lo van a conseguir con menos esfuerzo. 

Lo mismo la solución es que los ordenadores cuánticos busquen números primos más grandes aún, o volver a los mensajes romanos, yo qué sé. Por lo pronto, voy ahorrando para comprarme un ordenador de éstos, que pinta bien. 

José Pedro Martín Lorenzo