Fibonacci y sus conejos

¿Sois emprendedores? ¿Habéis pensado invertir en zonas rurales? Lo mismo estáis de suerte, porque tengo algo que proponeros. Un negocio, lo que estáis leyendo, concretamente una granja de conejos. 

No os vayáis, leedlo con atención, que igual tenéis delante de vuestros ojos la oportunidad de vuestras vidas. Os comento las condiciones, echamos cuentas y a lo mejor os interesa. 

Compramos una pareja de conejos recién nacidos para que se reproduzcan. Los conejos alcanzan la madurez sexual a la edad de un mes. En cuanto alcanzan la madurez sexual, los conejos se aparean y siempre resulta preñada la hembra. El periodo de gestación de los conejos es de un mes. Vamos a suponer que los conejos no mueren y que la hembra siempre da a luz una pareja de sexos opuestos. Los conejos tienen una moral y un instinto de variedad genética muy relajados y se aparean entre parientes.

Diréis que es mucho suponer, pero vamos a darlo por bueno. La pregunta que os haréis y que yo me he hecho es: ¿cuántas parejas de conejos habrá en la granja después de un año? ¿Cuándo empezamos a ganar dinero?

Vamos con los cálculos. 

Inicio del proceso: Nace la pareja de conejos (pareja A).

Fin del mes 1: La pareja A tiene un mes de edad. Se cruza la pareja A. 1 pareja que había + 0 parejas que han nacido = 1 pareja de conejos.

Fin del mes 2: La pareja A da a luz a la pareja B. Se vuelve a cruzar la pareja A. 1 pareja que había + 1 pareja que ha nacido = 2 parejas de conejos.

Fin del mes 3: La pareja A da a luz a la pareja C. La pareja B cumple 1 mes. Se cruzan las parejas A y B. 2 parejas que había + 1 pareja que ha nacido  = 3 parejas de conejos. 

Fin del mes 4: Las parejas A y B dan a luz a D y E. La pareja C cumple 1 mes. Se cruzan las parejas A, B y C. 3 parejas que había + 2 parejas que han nacido = 5 parejas de conejos. 

Fin del mes 5: A, B y C dan a luz a F, G y H. D y E cumplen un mes. Se cruzan A, B, C, D y E. 5 parejas que había + 3 parejas que han nacido = 8 parejas de conejos. 

Os dejo un dibujito que posiblemente os ayude. 

Podríamos seguir, pero creo que se intuyen los cálculos.

¿Cómo lo véis? Al terminar el año tendríamos 233 parejas de conejos. Ahora habría que ver precios de mercado, cuántas parejas vendemos, cuántas dejamos… 

Vaya cosas que se me ocurren, ¿verdad? “Este tío está pa’llá”, eso es lo que estáis pensando, pájaros. Yo creo que también sois un poco haters. Pues no es cosa mía, es como presentó la sucesión que lleva su nombre un tal Fibonacci en su libro Liber Abaci, publicado en 1202. 

Leonardo Pisano o Leonardo de Pisa, también conocido como Fibonacci, nació en 1170 y murió en 1240. Fue un divulgador y estudioso de la matemática indo-arábiga aprendida en sus visitas a distintas ciudades del Mediterráneo y desconocida en Occidente por entonces.

La definición de la sucesión de Fibonacci es muy sencilla, comienza con dos números naturales (con 0 y 1 en ciertos casos, otros la inician con 1 y 1) y a partir de estos, “cada término es la suma de los dos anteriores”. Esto es lo que se llama en matemáticas definición por recurrencia. 

Los primeros términos de la sucesión son: 0,1,1,2,3,5,8,13,21,34, 55, 89, 144, 233, 377, 610, 987, 1597,…

Esta sucesión, aparentemente inventada por Fibonacci, como normalmente pasa en estos casos, era conocida muchos años antes. La primera constancia escrita se le atribuye a Pingala, un matemático indio del siglo III a. C. nada más y nada menos. Cuidadín con los indios que aparecen mucho por aquí.

Lo curioso de esta secuencia es que tras una apariencia inocente, está presente en numerosos elementos en la naturaleza, así como en múltiples aplicaciones en ciencias de la computación, música, matemáticas, tendencias bursátiles o teoría de juegos, entre otras. De hecho, existe una publicación especializada llamada Fibonacci Quarterly[ dedicada al estudio de la sucesión de Fibonacci y temas afines.

Quizás lo más sorprendente sea su aparición en configuraciones biológicas:  

El ejemplo que se cita con más frecuencia es la flor del girasol, cuya gran mayoría posee 34 espirales en un sentido y 55 en el otro, o bien 55 y 89 respectivamente.

Las piñas, prácticamente cualquier variedad que encontremos, también presentan un número de espirales que coincide con dos términos de la sucesión de los números de Fibonacci, por lo general 8 y 13 o 5 y 8.

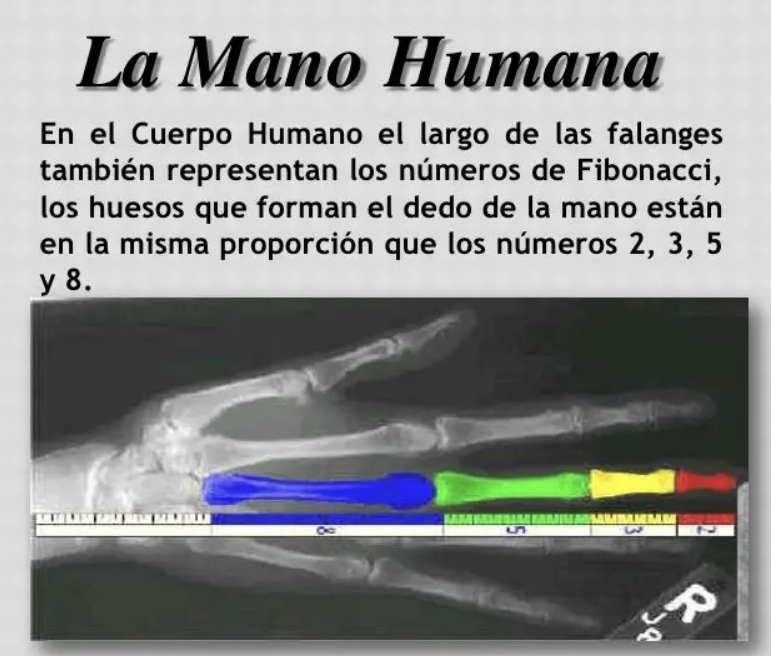
En nuestro cuerpo.

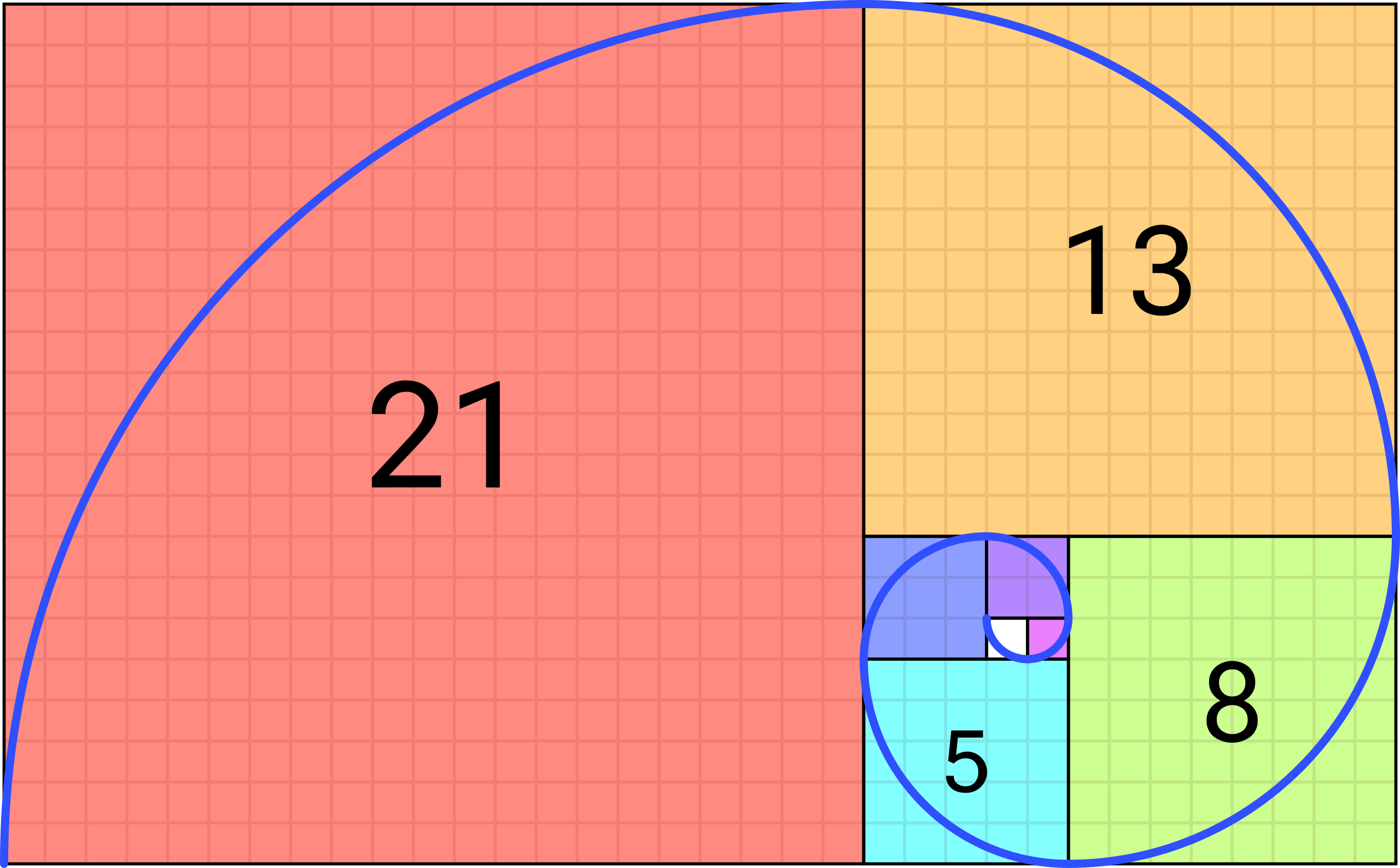
Con los números de la sucesión se puede crear la espiral de Fibonacci, la cual se genera dibujando arcos circulares uniendo las esquinas opuestas de los cuadrados de lado los valores de la sucesión; teselando sucesivamente cuadrados de lado 1, 1, 2, 3, 5, 8, 13, 21 y 34.

Bien, pues casualmente tienen esta estructura espiral el caparazón de algunos moluscos, como el nautilus, la dinámica de los huracanes o la organización de las galaxias. 

Supongo que sorprendidos, yo también lo estoy, pero es que no os he contado lo mejor, que es la relación que guarda esta sucesión con el número de oro. Pero eso amigos, será en otro capítulo de el hater, hasta entonces vamos pensando si montamos la granja de conejos o no… Salud para todos.