¿Cuántas primitivas distintas se pueden echar?

No sé si os habéis hecho alguna vez la pregunta de cuántas apuestas de la primitiva se pueden hacer o cuántas quinielas de fútbol. Supongo que alguno de vosotros lo habréis buscado por internet; y sí, son muchas… En matemáticas hay precisamente una disciplina, la combinatoria, que se encarga de este tipo de recuentos. Es la rama de las matemáticas que estudia las diferentes formas en que se pueden organizar, seleccionar o contar elementos dentro de un conjunto, por decirlo de alguna manera más o menos entendible. 

Para mí, la combinatoria es una corta rollos, porque uno va con toda la ilusión del mundo a echar su boleto y es como el diablo en el hombro susurrándote “tienes una posibilidad entre no sé cuántos millones, no te va a tocar”. Eso genera mala leche, mejor no saberlo. Por descontado que es difícil, pero y si sí, como dice aquel… Las matemáticas como siempre, tocando lo que no hay. 

Antes de empezar hoy, tenemos que saber qué es el factorial de un número y qué son los números combinatorios porque si no, no podemos avanzar. 

Se define el factorial de 5 y se denota como 5!, a la multiplicación 5·4·3·2·1, es decir:

5! =  5·4·3·2·1 = 120

Se define el número combinatorio 7 sobre 4 y se denota como: 

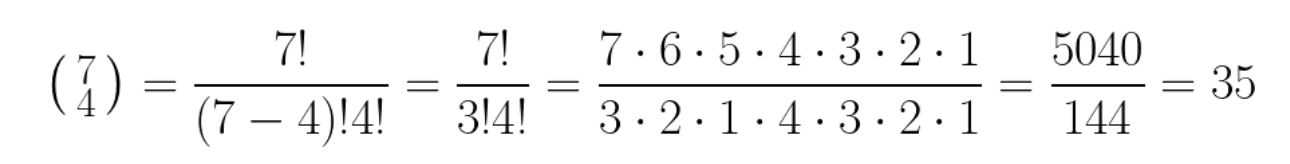
El de arriba siempre tiene que ser mayor o igual que el de abajo. 

También vamos a recordar, por si alguien anda despistado, que la potencia 5 elevado a 3 es un producto y se denota como: 

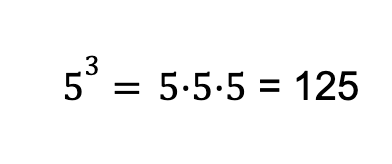
No os asustéis con las fórmulas porque las cuentas os las voy a dar hechas, tranquilos.

Dicho esto, vamos a ver las formas que tenemos de contar elementos de un conjunto. La primera pregunta que debemos hacernos es: ¿importa el orden?

A qué nos referimos con esto, pongamos algún ejemplo: 

En la final de los juegos olímpicos de 400 m.l. corren ocho atletas, ¿de cuántas formas diferentes se pueden repartir las medallas? Aquí sí importa el orden en el que llegan los tres primeros, no es lo mismo conseguir un oro que una plata. 

En cambio, la junta directiva de la asociación de vecinos de vuestro barrio está formada también por ocho integrantes y tres de ellos deben ser vocales. Entre los ocho, de cuántas formas diferentes se pueden asignar los cargos de vocales. En este caso no importa el orden, el grupo de vocales de esta directiva sería el mismo si sale Julio, Andrea y Sergio que si los elegidos son Sergio, Julio y Andrea. Este grupo de tres sólo debe contarse una vez. 

En función de la respuesta a si importa el orden o no, las técnicas de conteo las dividiremos: Variaciones o Combinaciones. 

• Sí importa el órden: Variaciones

• No importa el orden: Combinaciones

Dentro de las variaciones debemos hacernos una segunda pregunta: ¿intervienen todos los elementos?

Sigamos con la final de los 400 m.l. de los Juegos Olímpicos. Si sólo nos interesan de cuántas maneras posibles se pueden repartir las medallas, en este caso sólo intervienen 3 elementos de los 8 corren la final. Pero si queremos saber de cuántas formas diferentes pueden ocupar las posiciones de la primera a la última, ahora sí intervienen todos los elementos. 

• Variaciones

• No intervienen todos los elementos: Variaciones.

• Sí intervienen todos los elementos: Permutaciones.

Aquí nos encontramos con un exceso de notación y llamaremos variaciones a las agrupaciones en las que importa el orden y no intervienen todos los elementos y permutaciones cuando importa el orden e intervienen todos los elementos. 

Y por último nos podemos hacer una tercera pregunta, ¿se pueden repetir los elementos?

En nuestro ejemplo de la final, no se pueden repetir, el atleta que llega primero, no puede ser tercero en esa misma competición, en cambio, si nos preguntamos cuántos números de 3 cifra podemos construir con los dígitos 1,2,3,4,5,6,7,8. En este caso los dígitos sí se pueden repetir, por ejemplo tenemos 222, el 2 se repite tres veces.  

De esta manera nos vamos a encontrar técnicas de conteo con repetición y sin repetición.

A modo de resumen os dejo este cuadro de la wikipedia que es muy clarito:

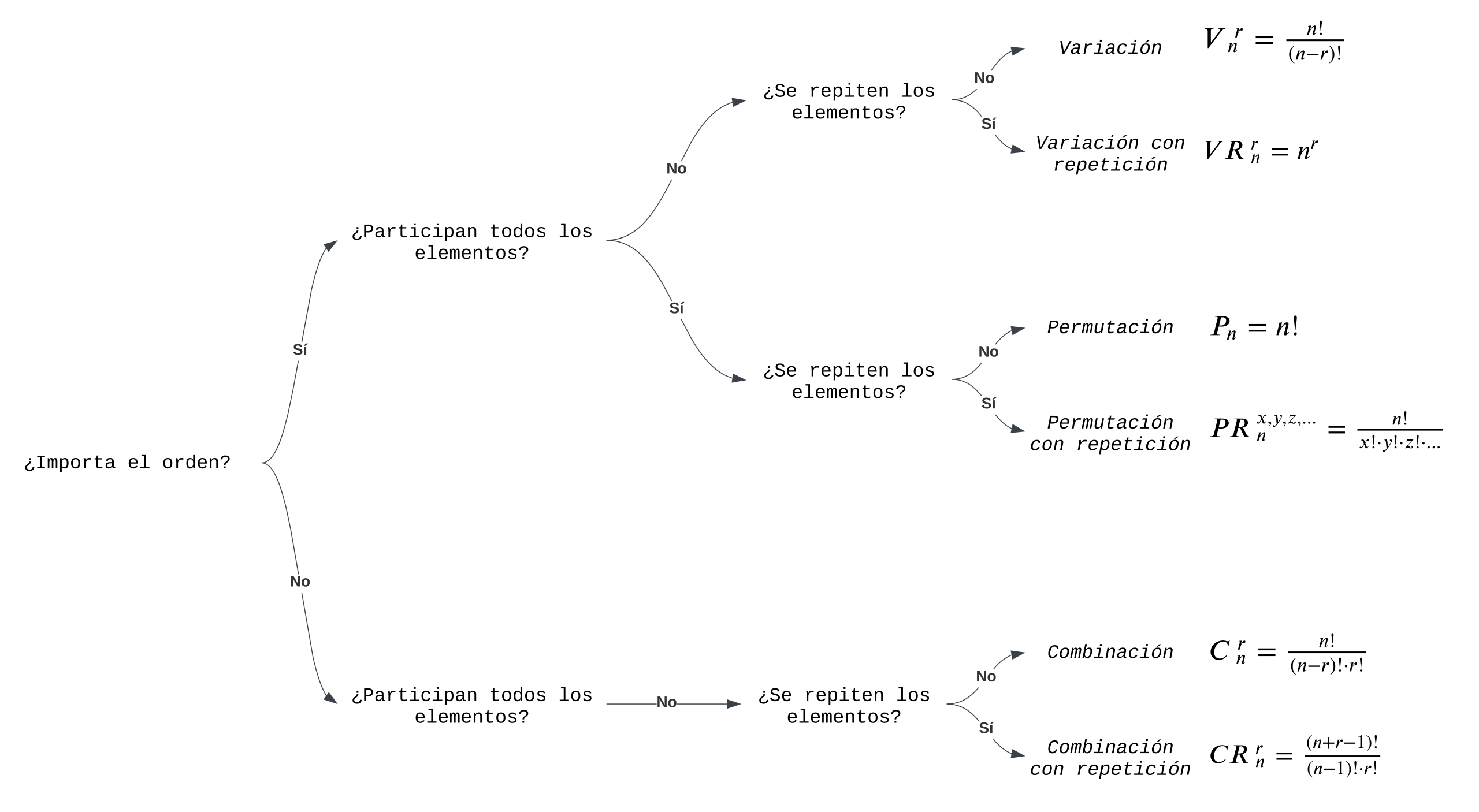
Ahora ya estamos en condiciones de ver los dos casos que os planteaba al principio, comencemos con el sorteo de la Primitiva. El juego consiste en elegir 6 números de 49.

Vamos a hacernos las tres preguntas mágicas: 

1.- ¿Importa el orden? Claramente no, da igual que en la combinación ganadora salga primero el 38 y luego el 26 que viceversa, lo importante es que que los tenga. Tenemos una Combinación.  

2.- ¿Intervienen todos los elementos? En las combinaciones nos da igual, esta pregunta es relevante en las variaciones, pero podemos contestarla de todos modos, no intervienen todos los elementos, sólo intervienen 6 de 49.

3. – ¿Se repiten los elementos? También es fácil de contestar, no se repiten, si elijo el número 36, no puedo volver a elegirlo. 

Entonces tenemos una Combinación sin Repetición de 49 elementos tomados de 6 en 6. 

En este momento estamos en condiciones de poder calcular el número de apuestas posibles de la primitiva:

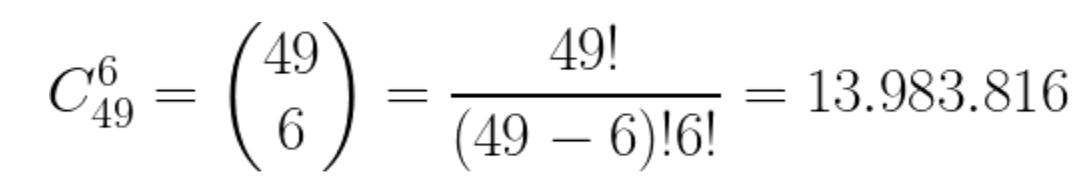
Ahí tenéis la primera decepción del día, si rellenamos un boleto simple tenemos una posibilidad de acertar entre más de 13 millones. 

Y la quiniela de fútbol… vamos a verla. 

En este juego nos proponen 15 partidos y hay que acertar, en cada uno de ellos, si gana el equipo local (1), empatan (X) o gana el equipo visitante (2).

Vamos a intentar responder a las tres preguntas:

1.- ¿Importa el orden? Aquí sí, no es lo mismo poner un 1 en el primer partido que en el segundo. Tenemos una Variación.  

2.- ¿Intervienen todos los elementos? No, hay 15 partidos y 3 resultados posibles.

3.- ¿Se repiten los elementos? Sí, podemos poner el 1 hasta 15 veces seguidas seguidas.  

En esta caso tenemos un Variación con Repetición de 3 elementos tomados de 15 en 15. 

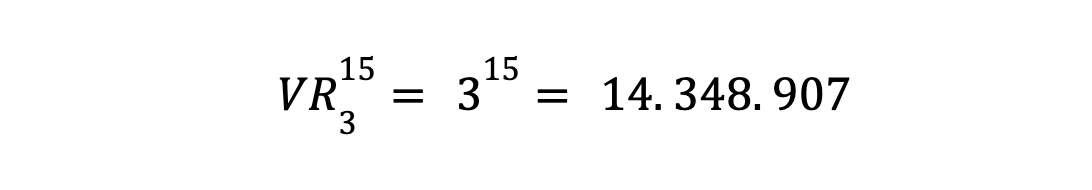
Peor todavía que la primitiva… si hacemos un boleto tenemos una posibilidad de acertar entre más de 14 millones… 

No me digáis que la combinatoria no es una tócame roque… pues para vuestra información, yo conozco a una familia que acertó los seis de la primitiva… gente de carne y hueso… anda, combinatoria, chúpate esa.

Que no os quiten nunca la ilusión, amigos haters.