Los números perfectos

Como bien sabéis los lectores de estos artículos, entre los amantes de las matemáticas nos encontramos en algunas ocasiones con gente ociosa que les gusta emplear su tiempo en buscar regularidades que son totalmente improductivas. Hoy os traigo un ejemplo de ello, qué le vamos a hacer, unos componen canciones y otros se dedican a buscar números perfectos.

Para ponernos en situación nos tenemos que retrotraer a comienzos del siglo II de nuestra era, sobre el año 100 d. C. Por aquella época el filósofo y matemático seguidor de la corriente neopitagórica imperante, Nicómaco Gerasa en su obra “Introducción a la aritmética”, no se le ocurrió otra que clasificar a los números naturales en tres categorías: abundantes, deficientes o perfectos.

Pero antes de entrar en la definición de cada uno de estos tipos de números debemos recordar qué consideramos en matemáticas que un número sea divisor de otro.

Un número a es divisor de otro b si al dividir b entre a la división es exacta, es decir, el resto de la división euclídea es cero. 

Por ejemplo, 3 es divisor de 6 porque al dividir 6 entre 3 la división es exacta ya que el cociente es 2 y el resto el 0 (6 = 3 · 2 + 0).

En este contexto, decimos que un número natural mayor que 1 es primo si sus únicos divisores son él mismo y el 1. Seguro que recordáis los primeros números primos: 2, 3, 5, 7, 11,…  

Para terminar de situarnos necesitamos saber que se consideran divisores propios de un número natural a todos los divisores naturales de ese número excepto él mismo. 

Ejemplo, los divisores naturales de 10 son 1, 2, 5 y 10 pero los divisores propios de 10 son 1, 2 y 5.

Yo creo que con esto ya podemos tirar p’alante. 

Volvamos entonces a Nicómaco Gerasa a su especialmente singular clasificación de los números, según él podían ser: 

• Abundantes. Aquellos en que la suma de divisores propios es más grande que el propio número.

• Deficientes. Los que la suma de los divisores propios es más pequeña que el propio número.

• Perfectos: Aquellos en que los divisores propios suman exactamente el propio número.

 Veamos un número de cada tipo para que no quede ninguna duda. 

Los divisores del 12 son: 1,2, 3, 4, 6, 12. Los divisores propios serán todos menos el propio número, es decir: 1, 2, 3, 4, 6. Si sumamos estos números, obtenemos: 1+2+3+4+6 = 16 que es mayor que 12, por lo que podemos decir que 12 es un “número abundante”.

Tomemos ahora otro número, por ejemplo el 32. Todos sus divisores son: 1, 2, 4, 8, 16 y 32. Por tanto sus divisores propios son: 1, 2, 4, 8 y 16. Si los sumamos todos tendremos: 1+2+4+8+16= 31. Como 31 es menor que 32, diremos que 32 es un “número deficiente”.

Por último, si tomamos el número 6, observamos como todos sus divisores son: 1, 2, 3 y 6. De estos los divisores propios serían: 1, 2 y  3. Si los sumamos, vemos fácilmente que obtenemos el número 6; así pues: 1+2+3 = 6. Por tanto, el número 6 es un “número perfecto”.

Una vez que tenemos claro qué son números perfectos, entiendo que vuestra duda (y la mía también, para qué os voy a engañar) es descubrir más números perfectos, si existe algún algoritmo para encontrarlos y todas esas mandangas que se les ocurre a esta gente. 

Podéis flipar porque en los Elementos de Euclides ya se explica un proceso para localizarlos consistente en: 

En primer lugar se toma la sucesión de potencias de 2: 1, 2, 4, 8, 16, 32,…. y comenzamos sumando los dos primeros números de la sucesión, después tres, después cuatro y así sucesivamente. Si esas sumas dan como resultado un número primo la multiplicamos por el mayor de los sumandos y el resultado, tachán, es un número perfecto. Vamos a verlo.  

• 1 + 2 = 3, como es primo, (1 + 2) · 2 = 3 · 2 = 6, que ya vimos que era perfecto.  

• 1 + 2 + 4 = 7, como es primo (1 + 2 + 4) · 4 = 7 · 4 = 28. Veamos que es perfecto. Los divisores propios de 28 son: 1, 2, 4, 7 y 14. Resulta que 1 + 2 + 4 + 7 + 14 = 28, número perfecto. 

• 1 + 2 + 4 + 8 = 15, no es primo, así que pasa palabra. 

• 1 + 2 + 4 + 8 + 16 = 31, es primo, sigamos entonces. (1 + 2 + 4 + 8 + 16) · 16 = 31 · 16 = 496, que podéis comprobarlo, es perfecto. 

• 1 + 2 + 4 + 8 + 16 + 32 = 63, no es primo… sigamos.

• 1 + 2 + 4 + 8 + 16 + 32 + 64 = 127, es primo, (1 + 2 + 4 + 8 + 16 + 32 + 64) · 64 = 127 ·64 = 8128 que es perfecto.

Si tenéis ganas podéis comprobar que 6, 28, 496 y 8128 son los primeros cuatro números perfectos, es más, este algoritmo es válido.

Aplicando la suma de los primeros términos de una progresión geométrica, el algoritmo dice lo siguiente: 

 

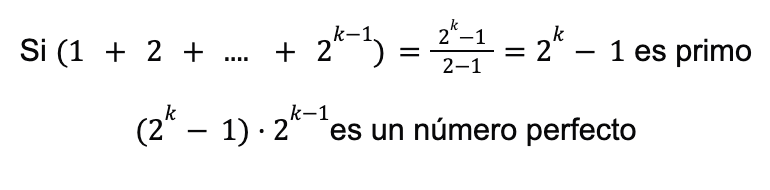
A estos números 

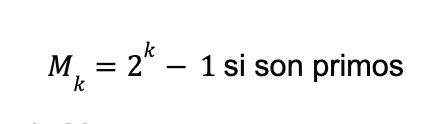
reciben el nombre de primos de Mersenne. 

Por lo que la búsqueda de números perfectos por este método se reduce a buscar números primos de Mersenne.

A día de hoy se conocen poco más de 50 números perfectos y según el teorema de Euclides-Euler (demostrado por Leonhard Euler, completando un trabajo de Euclides) establece que todos los números perfectos pares tienen la forma anterior, pero existe un problema abierto y es que se desconoce por completo si existe un número que cumpla la definición de perfecto y sea impar. Ahí os lo dejo, por si os queréis entretener. 

En fin, como os dije al principio, todo muy productivo, vamos que difícilmente podríamos vivir sin estos números. No sé a vosotros, pero a mí me han salvado la vida. 

Perfecto o casi perfecto era Robe, o mejor dicho, sus canciones, ese sí que era perfecto, DEP.