El número de oro (y III)

Con este artículo, os lo prometo, ya terminamos con el dichoso número de oro, que ya está bien. Pero puestos a hablar de él, no podía dejar atrás ni lo escrito en los dos primero artículos, aquí tenéis los enlaces (El número de oro (I) y El número de oro (II) de la sección de El hater matemático), ni lo que os quiero contar en éste sobre sus aplicaciones en la naturaleza y en el arte. 

Ya vimos, y si no os lo recuerdo, que el número áureo y Fibonacci (su sucesión) están íntimamente ligados, aquí también os dejo enlace al artículo de el hater Fibonacci y sus conejos para poneros en situación, en el sentido que si encontramos elementos de esta sucesión por ahí, de alguna manera ese ser, forma u objeto también está relacionado con el número de oro. 

Para terminar con la introducción, por si alguien anda perdido aún, el número de oro o el número áureo o la sección áurea o la divina proporción… conocido con las letras griegas φ (phi) (en minúscula) o Φ (Phi) (en mayúscula) era el número irracional 1,618… que cumplía un montón de propiedades numéricas y geométricas – hasta aquí habíamos llegado –  pero además de ese cúmulo de casualidades, resulta aparece en distintos elementos de la naturaleza.

Es tal el papel que juega el número áureo en distintas características de las plantas como la disposición de los pétalos de las flores o la distribución de las hojas en un tallo que en botánica tiene hasta una ley propia denominada la Ley de Ludwig.

Por otro lado si nos da por dividir el grosor del tronco de un árbol entre el de sus ramas principales, o el de las ramas principales entre las secundarias, el resultado se aproxima a Φ.

O para que las hojas esparcidas de una planta (filotaxis) o las ramas alrededor del tronco tengan el máximo de insolación con la mínima interferencia entre ellas, estas deben crecer separadas en hélice ascendente según un ángulo constante y teóricamente igual a 360° (2 – φ) ≈ 137º 30′ 28″, hecho que fue descubierto empíricamente por Church y confirmado matemáticamente por Weisner en 1875.

La concha del nautilus es un ejemplo clásico donde la relación de crecimiento de sus cámaras se rige por la secuencia de Fibonacci y el número de oro (φ ≈ 1,618). Esto significa que a medida que la concha crece en espiral, cada nueva cámara es un poco más grande que la anterior de una manera que mantiene la proporción áurea, dando lugar a la bella forma que vemos en la naturaleza.

Pero no solo en la concha del nautilus se da, si no lo podemos encontrar en las conchas del Fusus antiquus, del Murex, de Scalaria pretiosa, de Facelaria y de Solarium trochleare, entre otras, que siguen este tipo de espiral de crecimiento.

Si nos vamos al cuerpo humano existen algunas relaciones, al menos curiosas, que se aproximan a la proporción áurea. 

• La relación entre la altura total de una persona y la distancia desde el ombligo hasta el suelo.

• La división entre la distancia desde el hombro hasta la punta de los dedos y la distancia desde el codo hasta la punta de los dedos.

• La relación entre la distancia desde la cadera hasta el suelo y la distancia desde la rodilla hasta el suelo.

• El cociente entre la longitud de la mano y la de las falanges.

• Muchas de las proporciones consideradas estéticamente agradables en el rostro humano se dice que siguen la proporción áurea. Por ejemplo, la relación entre la longitud del rostro y el ancho, y la distancia desde la línea de los ojos hasta la boca en comparación con la distancia desde la línea del cabello hasta los ojos.

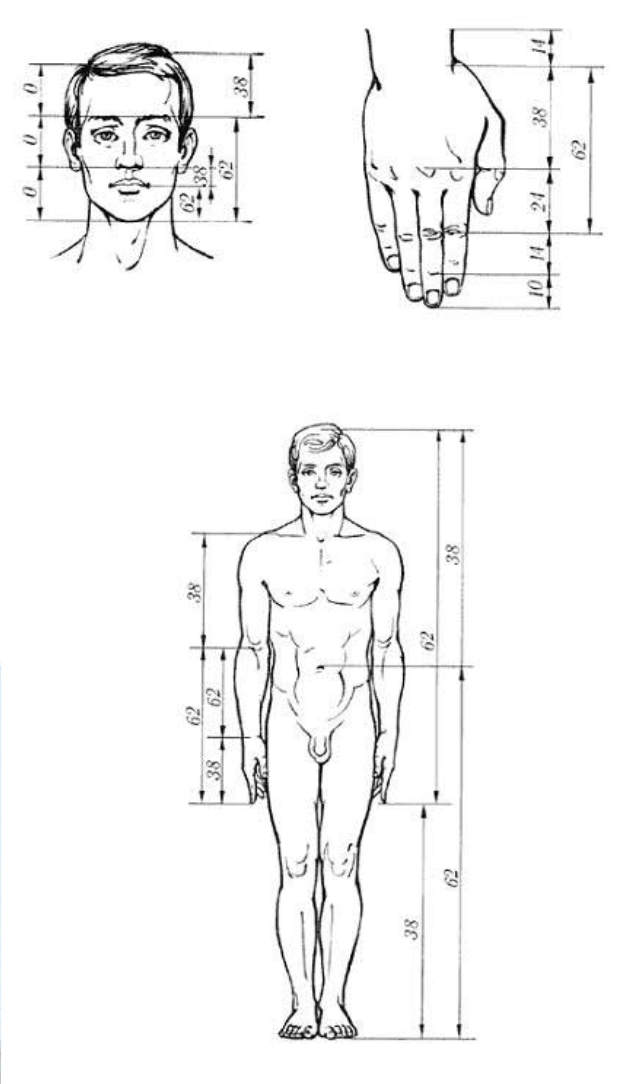
¿Todavía no habéis cogido el metro? No sé a qué estáis esperando.

Y podríamos seguir, pero os he prometido que este era el último artículo de esta serie, así que nos vamos al número de oro en el arte.

La Gran Pirámide de Guiza (también conocida como pirámide de Keops o de Jufu) es la mayor de las pirámides de Egipto y una de las siete maravillas del mundo antiguo. Fue ordenada a construir por el faraón Keops y se cree que su arquitecto fue Hemiunu.

Resulta que por lo visto la altura del monumento dividida por la mitad de la base es aproximadamente al número áureo. Además, las secciones en las que se divide la pirámide, como la altura hasta el punto medio y la cúspide, también cumplen dicha proporción. ¿Conocía Hemiunu el número de oro o le parecía estéticamente bella?

Estudios como los de Gustav Theodor Fechner responden a esta pregunta demostrando que a lo largo de la historia la percepción de la belleza radica en la proporción áurea. Por ello, aquello que matemáticamente más se aproxime a φ, se percibirá como más bello y perfecto. Esta noción de belleza y perfección es aplicable a estructuras arquitectónicas, pinturas, partituras musicales, fractales y personas.

El Partenón griego es otro ejemplo destacado en el que se dice que se aplicó el número de oro (o razón áurea, Phi ≈ 1,618) para lograr proporciones estéticas consideradas perfectas, con rectángulos áureos y espirales que se observan en la fachada y otros elementos arquitectónicos del templo griego. Aunque algunos estudiosos discuten la intencionalidad de su uso, la presencia de esta proporción es frecuente en la arquitectura clásica y se considera que contribuye a la armonía y belleza visual de la obra. 

El número áureo también aparece en la pintura, así queda plasmado en las relaciones de los objetos y personas que aparecen en las obras de Miguel Ángel, Durero, Leonardo Da Vinci o Velázquez, entre otros.

La Gioconda de Leonardo Da Vinci y Las Meninas de Diego Velázquez 

Y por último, para terminar, la divina proporción también está presente en composiciones musicales como las sonatas de Wolfgang Amadeus Mozart, en la Quinta Sinfonía de Beethoven o en obras de Schubert (que probablemente compusieron estas relaciones de manera inconsciente, basándose en equilibrios de masas sonoras) pero por debajo subyace la belleza, la armonía de este número al cual me rindo, lo reconozco… algo debe tener para que esté por todos lados, pero no os acostumbréis matemáticos y matemáticas del mundo, por esta vez, para vosotros la perra gorda. 

Sed felices.