
Los secretos del triángulo de Pascal
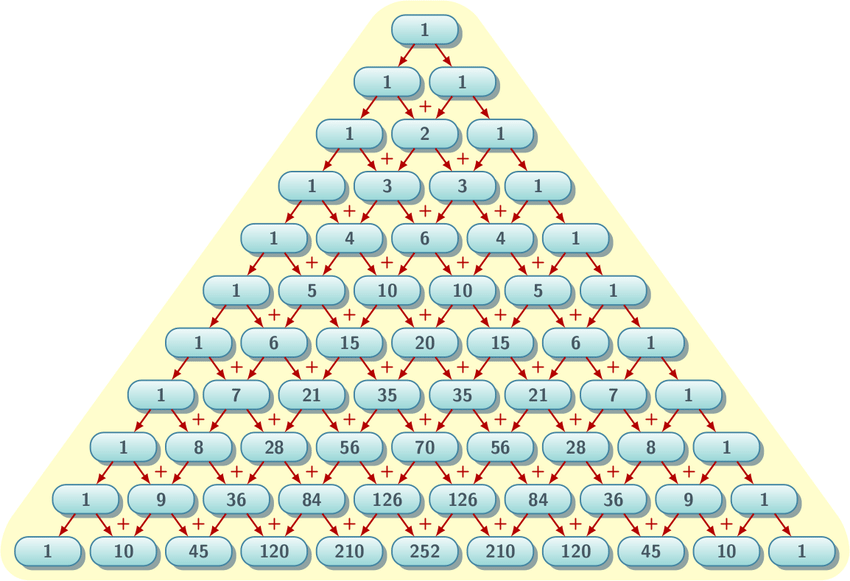
Esta semana en clase les he propuesto a mis alumnos realizar sumas, en la línea de Fibonacci, pero intentando que quedase bonito, de manera que les he planteado que fuésemos colocando los resultados en forma triángulo, construyéndolo de arriba hacia abajo.
Si tenéis a mano lápiz y papel, os animo a que lo creéis vosotros, es muy divertido y fácil. Además veréis la que vamos a liar con este insignificante jueguecillo.
Es un triángulo numérico en el que cada número es la suma de los dos que están justo encima de él. Se construye fila por fila, empezando por el número 1 en la cima.
Flia 0: Sólo el número 1
Fila 1: Comienza y termina con 1.
Fila 2: Empieza y termina con 1. El número del medio se obtiene sumando los dos números de arriba: 1 + 1 = 2.
Fila 3: Empieza y termina con 1. Los del medio se calculan sumando 1 + 2 = 3 y 2 + 1 = 3
Y así sucesivamente…
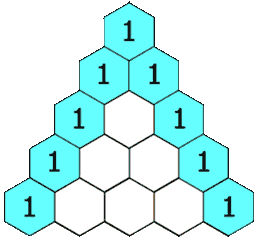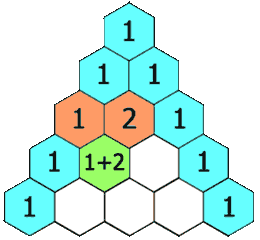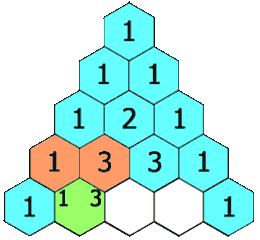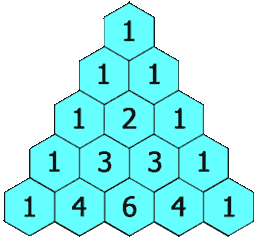
¿Queda bonito, verdad? Siento deciros que esto no es cosa mía, viene de largo y como seguro que os podéis imaginar este triangulito tiene hasta nombre propio. Y no uno, sino muchos. El primero en escribir sobre él fue un viejo conocido nuestro, Pingala, por el 200 a.C. Más tarde los hindúes decidieron llamarlo la escalera del Monte Meru, los persas el Triángulo de Khayyam, los chinos el Triángulo de Yang Hui. En Italia se le conoce como el Triángulo de Tartaglia, en honor al algebrista italiano Niccolò Fontana Tartaglia (1500–1577). En el Tratado del triángulo aritmético (otro nombre) publicado en 1654, el francés Blaise Pascal reúne varios resultados ya conocidos sobre el triángulo, y los emplea para resolver problemas ligados a la teoría de la probabilidad, gracias a ello recibe el nombre más extendido, el Triángulo de Pascal. Ya sabéis lo que le gusta a un matemático que algo lleve su nombre.
El triángulo se puede seguir construyendo indefinidamente pero para que tengáis una idea clara de cómo queda os dejo uno hasta la fila 10.

Lo alucinante de este triángulo, aparentemente inocente, es que esconde un montón de patrones que han sorprendido al mundo matemático a lo largo de la historia, veamos algunos.
Si sumamos los numerosos que forman cada fila nos encontramos con lo siguiente:
Fila 0 = 1
Fila 1 = 1 + 1 = 2
Fila 2 = 1+ 2 + 1 = 4
Fila 3 = 1 + 3 + 3 + 1 = 8
Fila 4 = 1 + 4 + 6 + 4 + 1 = 16
Os suena verdad…
Fila 5 = 32, Fila 6 = 64, Fila 7 = 128 …
Efectivamente son las potencias de 2.
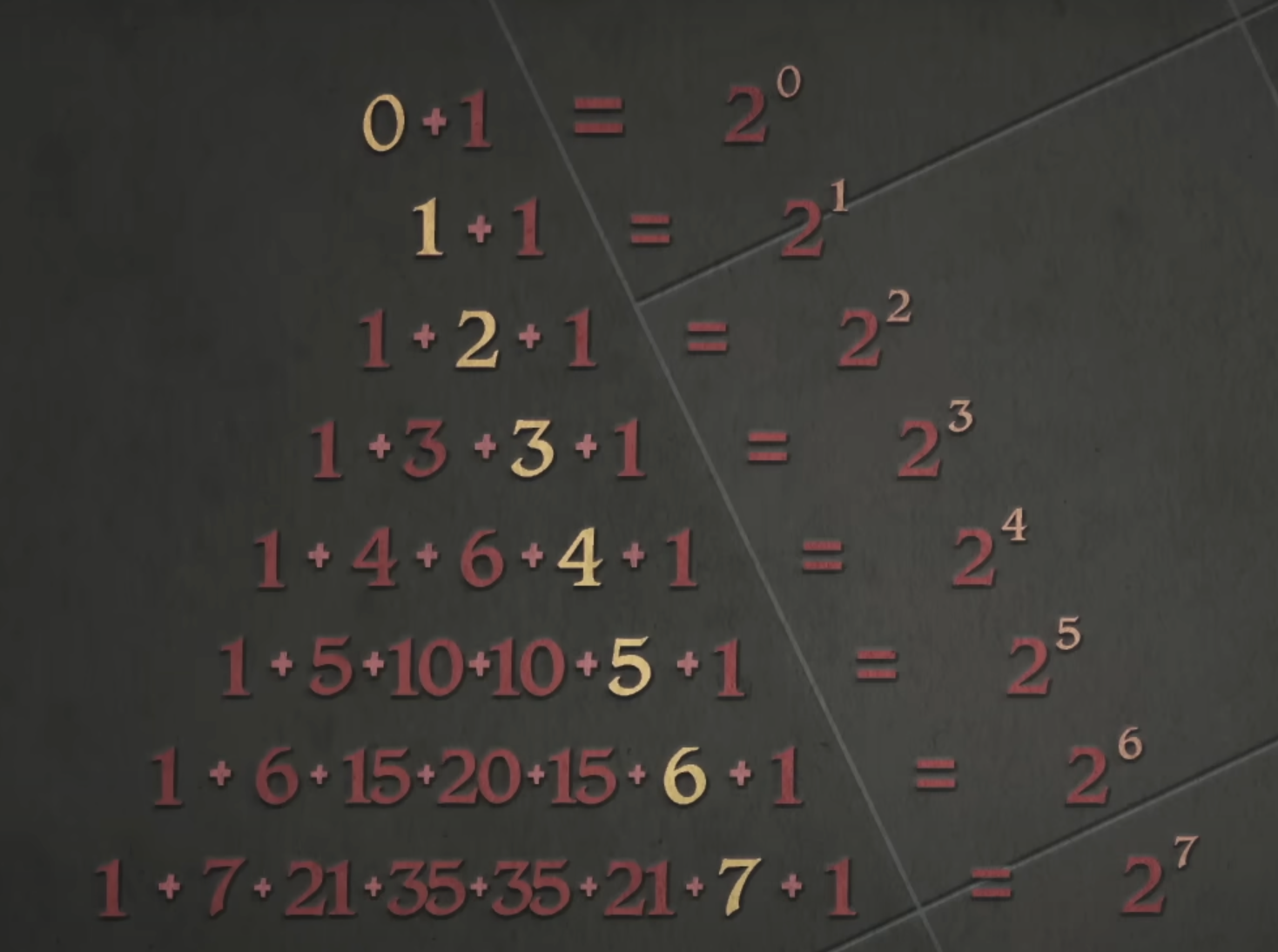
Si seguimos con las filas y a cada número le asignamos un orden de derecha a izquierda, es decir, al que está más a la derecha la unidades, al siguiente la decenas…. y lo sumamos nos queda:
Fila 0 = 1 x 1 = 1
Fila 1 = 1 x 10 + 1 x 1 = 11
Fila 2 = 1 x 100 + 2 x 10 + 1 x 1 = 121
Fila 3 = 1 x 1.000 + 3 x 100 +3 x 10 + 1 x 1 = 1.331
Fila 4 = 1 x 10.000 + 4 x 1.000 + 6 x 100 + 4 x 10 + 1 x 1 = 14.641
Fila 5 = 1 x 100.000 + 5 x 10.000 + 10 x 1.000 + 10 x 100 + 5 x 10 + 1 x 1 = 161.051
….
Visto lo visto, si me lo tuviera que jugar a algo, me lo jugaría al 11.
Equilicuá, es cada una de las sucesivas potencias de 11.
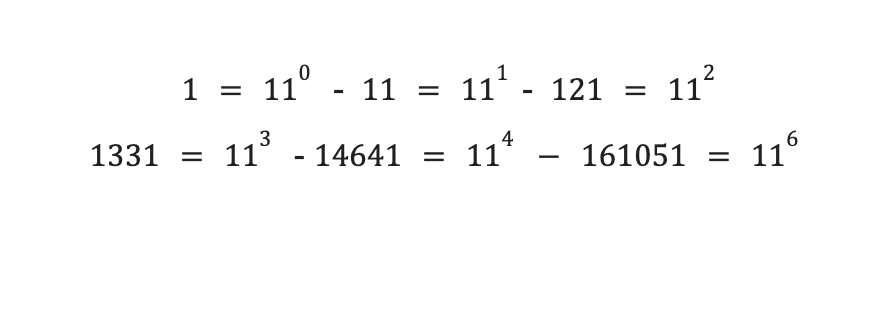
Si nos fijamos ahora en las diagonales, las dos primeras no son muy llamativas, la exterior son todo unos y la segunda los números enteros positivos: 1,2,3,4,5,… pero fijaos en la tercera:

Son los llamados números triangulares y cuentan los objetos dispuestos en forma de triángulo equilátero.
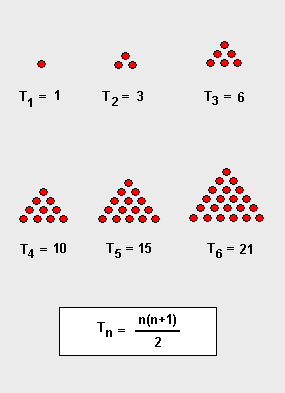
Y la siguiente: 1, 4, 10, 20, 35, 56, 84, 120 son los números tetraédricos porque de la misma forma cuentan los objetos dispuestos en forma de tetraedro (pirámide).
Cuidadín con el triangulito que se las trae.
Qué os parece si sólo nos quedamos con los números impares, vamos a sombrearlos a ver qué pinta tiene:

En este caso se obtiene un fractal muy famoso, el Triángulo de Sierpinski, que es una movida matemática que se inventó un polaco con este apellido que consiste en unir los puntos medios de cada lado y arrancar el triángulo central interno y así sucesivamente con los triángulos que nos van quedando. Pero este triángulo se lo imaginó Sierpinski en el siglo XX y el triangulito ya estaba dando vueltas mucho tiempo antes.
En el artículo de el hater ¿Cuántas primitivas distintas se pueden echar? dijimos que éstas se calculaban gracias a la combinatoria, concretamente eran combinaciones sin repetición de 49 números posibles tomados de 6 en 6.
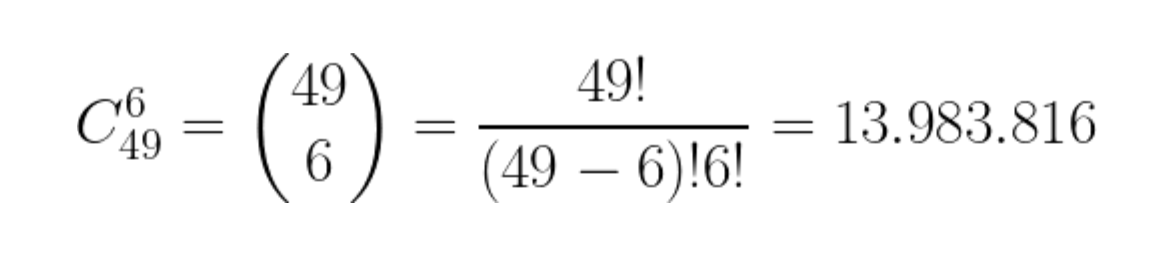
Pues resulta que todos los números del Triángulo de Pascal son números de este tipo. Combinaciones sin repetición, como la primitiva.

Y claro, una de las aplicaciones más usuales de estos números son los coeficientes del desarrollo de las potencias de un binomio, de manera que el Triángulo de Tartaglia esconde este otro secreto.
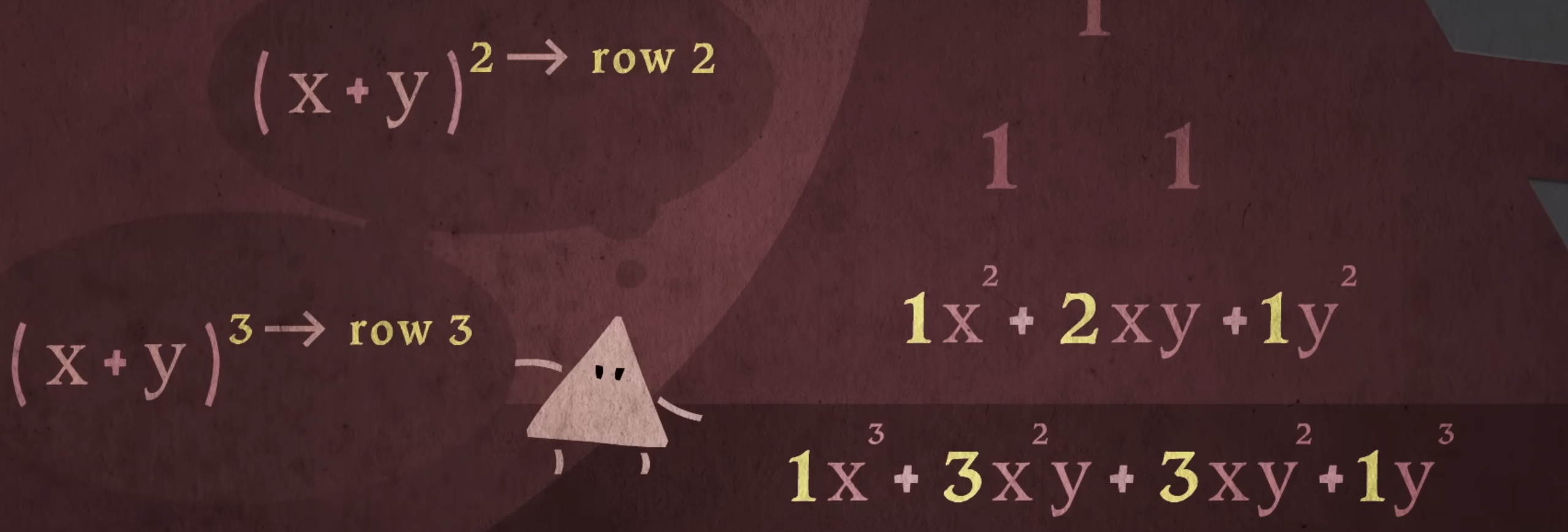
Y sigue y sigue, de hecho a día de hoy están apareciendo más aplicaciones y patrones que tiene escondidos…
Os voy a dejar, a ver si encuentro algo novedoso y lo mismo empiezan a llamarlo el Triángulo de El Hater.
























