El juego de la casita

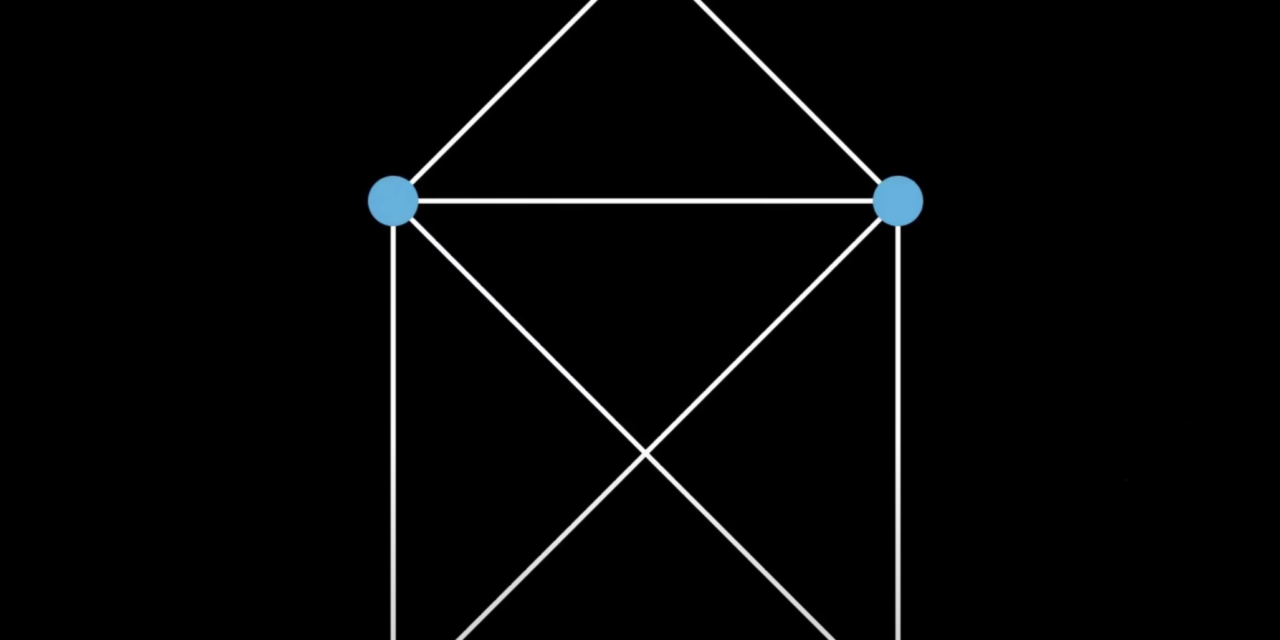
Seguro que alguna vez os han propuesto resolver el juego de la casita, que consiste en dibujarla de un solo trazo, sin levantar el lápiz del papel ni pasar dos veces por la misma línea. ¿Fuisteis capaces de hacerlo? Os lo dejo aquí para intentarlo de nuevo o por si es la primera vez que os enfrentáis a él. 

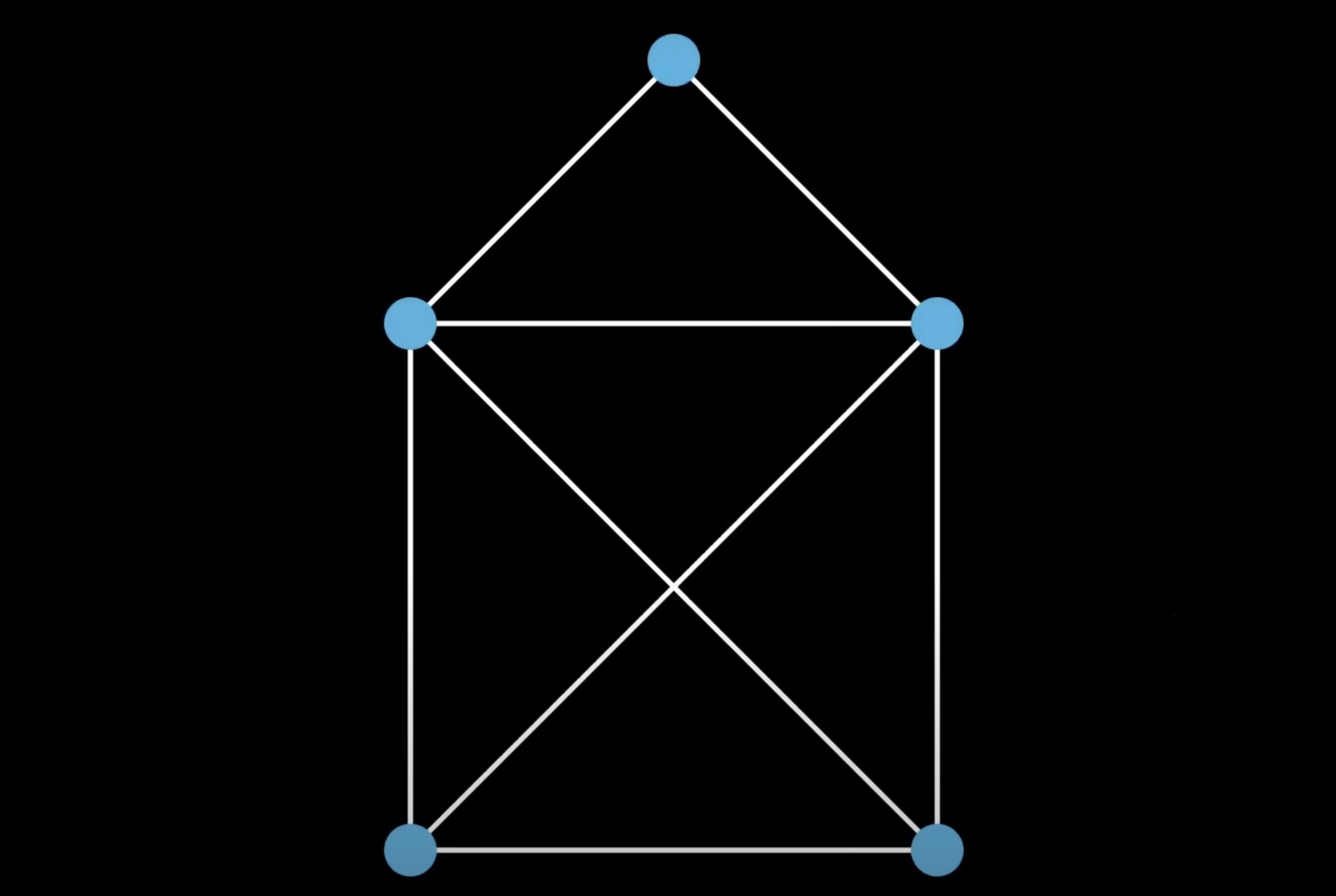
Esto que veis en matemáticas se llama grafo y lo descubrió un tal Leonhard Euler que allá por el siglo XVIII le dio por preguntarse si se podía realizar un paseo por la ciudad de Königsberg atravesando sus siete puentes pasando una sola vez por cada uno de ellos.  

Que digo yo que ya tenía tiempo este hombre y debía estar ocioso para preguntarse esto. Es como cosa de jubilados, ¿no? En fin, los matemáticos son muy raros, ya os habréis dado cuenta después de los artículos que llevamos de el hater. 

La situación era más o menos como se muestra en el gráfico: 

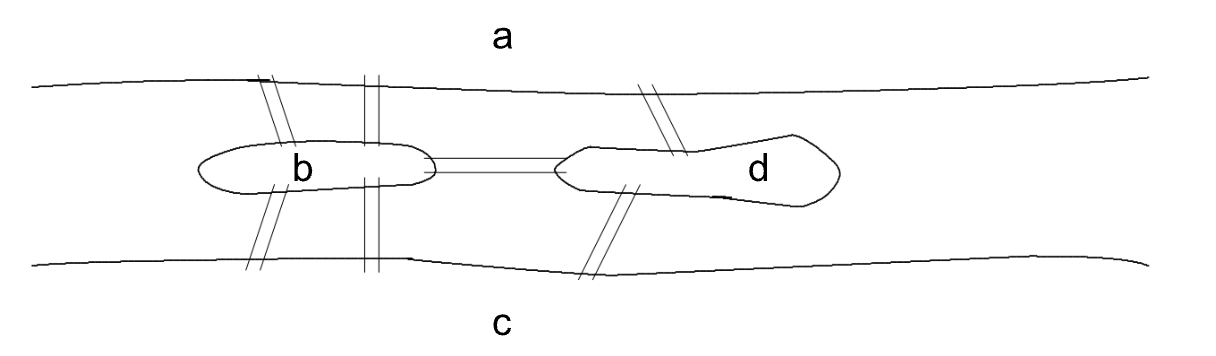
El río Pregel dividía la ciudad en dos partes, dejando una a cada orilla y además existían dos pequeñas islas conectadas, como se muestra, con dichas orillas y entre ellas a través de esos siete puentes. 

A Leo le dio por representar cada una de las cuatros zonas (las dos orillas y las dos islas) por puntos y los puentes que las unían por líneas, planteando un gráfico de este estilo.

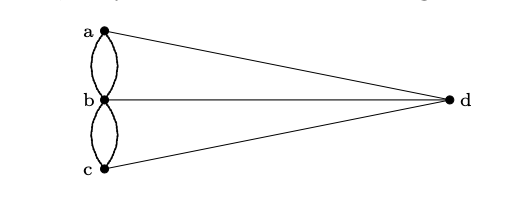
Este problema es conocido como el de los puentes de Königsberg y sienta las bases de la teoría de grafos cuyo padre ya os podéis imaginar quién fue y su trabajo sobre este problema, titulado Solutio problematis ad geometriam situs pertinentis[ (La solución de un problema relativo a la geometría de la posición) en 1736, es considerado el primer resultado importante sobre ella.

Decir, como curiosidad, que Königsberg pertenecía a la antigua Prusia Oriental en aquella época y es actualmente la ciudad rusa de Kaliningrado.

Antes de ver si el problema de los puentes de Königsberg o el de la casita tienen solución, veamos qué entendemos por grafo.

Un grafo es una estructura formada por puntos (llamados nodos o vértices) conectados entre sí mediante líneas (llamadas aristas o arcos).

Vamos a familiarizarnos con ello, los puntos son nodos a partir de ahora y las líneas son aristas. ¿Todo el mundo centrado? Sigamos. 

Ahora abramos nuestra mente. Si en un mapa representamos las ciudades como nodos y las carreteras que las unen como aristas, tenemos un grafo. En las redes sociales, si cada uno de los usuarios es un nodo y la conexión entre dos de ellos  una aristas, ahí hay otro grafo, o si estimamos oportuno identificar las páginas web como nodos y los enlaces entre ellas como aristas, equilicuá, otro grafo al canto. Por lo que ya os podéis ir haciendo una idea de las aplicaciones que tiene este campo en múltiples disciplinas. Pero no nos adelantemos…

Estábamos con los puntitos y las líneas, perdón, con los nodos y las aristas. Llamaremos grado del nodo al número de aristas que llegan a cada uno. Veámoslo con los ejemplos de la casita y con el de los puentes. 

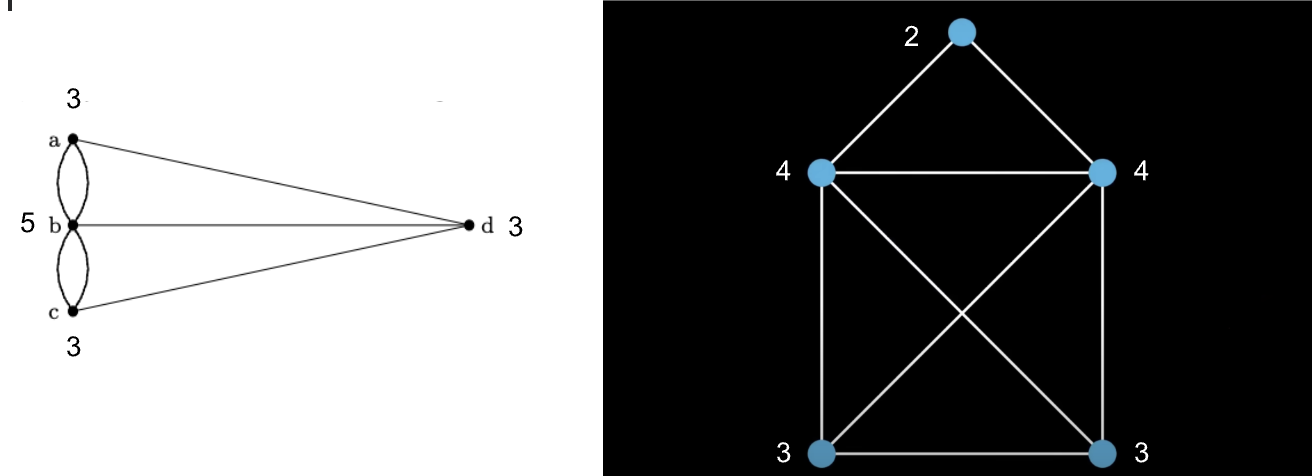
Para seguir con el rigor matemático, llamaremos camino euleriano al recorrido por un grafo que pasa exactamente una vez por cada arista, sin repetir ninguna. Justo lo que queremos con el problema de la casita y con el de los puentes. 

Y ya la última, diremos que un grafo es conexo si entre cualquier par de nodos existe un camino que los une. Da igual los que se elijan. 

Pues el pájaro este de Euler, que no tenía un pelo de tonto, demostró el siguiente resultado: 

Un grafo conexo tiene un camino euleriano si y sólo si tiene exactamente 0 o 2 vértices de grado impar.

• Si todos los vértices tienen grado par, entonces existe un ciclo euleriano (empieza y termina en el mismo vértice).

• Si tiene exactamente dos vértices de grado impar, entonces existe un camino euleriano (empieza en un vértice impar y termina en el otro).

• Si hay más de dos vértices de grado impar, no existe camino euleriano que valga (y ya os digo que no puede existir un solo nodo con grado impar, es imposible). 

Y la demostración no es muy compleja: en los nodos intermedios, tenemos que entrar por una arista y salir por otra, por lo que el grado siempre debe ser par. Y solo podrían ser de grado impar los nodos inicial, por donde salimos y final, donde termina. Si todos los nodos tienen grado par, salimos y llegamos al mismo, por lo que en este caso tenemos un ciclo.  

Con este resultado ya tenemos solución para el problema de la casita y el de los puentes. Los grados de los nodos de la casita son: 3,3,4,4,2. Dos impares y tres pares, por lo que por el resultado de Euler – uno de los muchos que tiene – existe solución y la casita se puede pintar sin levantar el lápiz del papel pasando una vez por cada arista. En cambio, por mucho tiempo que le dediquéis, el problema de los puentes de Königsberg no hay tu tía. 

Pero claro, esto no queda aquí, la teoría de grafos empezó a desarrollarse, así podemos encontrar grafos dirigidos, que son aquellos en los que se le asigna un sentido a las aristas, representadas con flechas. De esta manera, podemos encontrarnos con aristas en los dos sentidos o únicamente uno. Un ejemplo es la red social X, los usuarios son los nodos y las aristas apuntan a las personas que siguen. Por ejemplo, a Cristiano Ronaldo le llegan muchas aristas pero de él sale la que se dirige hacia Georgina y poco más.

A las aristas también se les puede asignar un peso o valor. El ejemplo más usual, aunque no el único, es un mapa de carreteras. Los nodos son las poblaciones y las aristas las carreteras que las unen, asignándole a cada arista como peso la distancia que separa dichas localidades. Supongo que a alguno de vosotros ya se os habrá encendido la bombilla y os habrá venido a la cabeza el problema del viajante del que hablamos en el artículo de el hater: Las hormigas enseñan a los matemáticos. Llegar de un sitio a otro, pasando por donde tengamos que pasar, realizando la mínima cantidad de kilómetros. 

Las aplicaciones de la teoría de grafos son innumerables y una de las ramas, que no la única, que ha contribuido con más notoriedad al desarrollo de la inteligencia artificial.

Este artículo servirá de base para hablaros de algunas de ellas que a el hater le parecen reseñables, pero será otro día, como siempre en domingo. 

Sed buenos