Las hormigas enseñan a los matemáticos

Hoy os traigo un problema, uno clásico, dicen por ahí que posiblemente sea el más difícil del mundo y ¿sabéis quién ha dado una de las mejores soluciones hasta el momento? Las matemáticas… no, las hormigas, bueno, o las hormigas con la ayuda de las matemáticas, o las matemáticas inspiradas en el comportamiento de las hormigas… No sé, os lo cuento y vosotros decidís.
El reto al que me refiero es El Problema del Viajante, que dice: Un viajante debe visitar un conjunto de ciudades conocidas las distancias entre cada par de ellas, ¿cuál es la ruta más corta posible que visita cada ciudad exactamente una vez y al finalizar regresa a la ciudad origen?
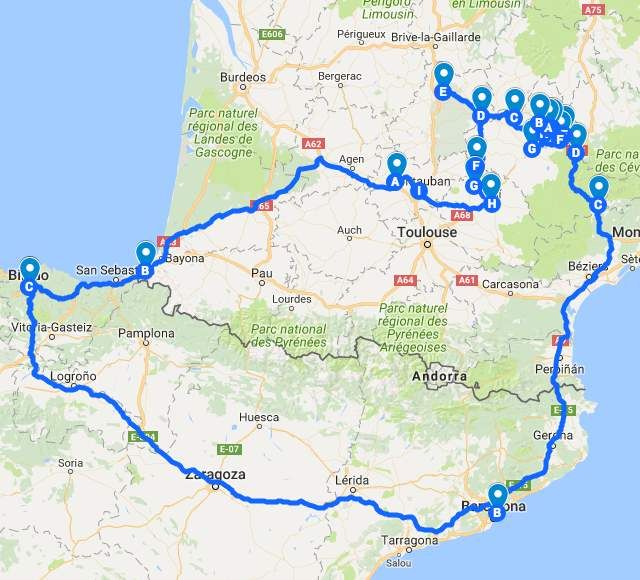
Puede parecer un problema sencillo con una solución casi de perogrullo, sumamos los kilómetros de todas las rutas posibles existentes y nos quedamos con la más corta. Listo, hasta la semana que viene…
No vais a tener esa suerte, sigo dándoos la matraca. Hay un ligerísimo detalle a tener en cuenta, el número de rutas posibles crece de forma demoniacamente rápido a medida que el número de ciudades aumenta un poquito.
Para 5 ciudades hay 12 rutas, pero con 12 ciudades ya nos encontramos con 19.958.400 de rutas posibles y si nos vamos a 20 ciudades la broma sube a 60 mil billones de rutas, imaginaos que calcular los kilómetros de cada una de ellas para quedarnos con la más corta no es la mejor idea. El número de rutas posibles en función del número de ciudades es (n-1)!/2, siendo n el número de ciudades, por si os pica la curiosidad de cómo hemos hecho los cálculos.
Pero es que el problema del viajante no sólo se usa para optimizar rutas de transporte, sino también en el diseño de circuitos electrónicos o en logística de supermercados y grandes almacenes, entre muchas otras aplicaciones y claro, ahí el número de “ciudades”, “estantes” o como se llame en cada caso no son pocas. Y entonces, ¿qué hacemos?
Hay dos posibles opciones, que los matemáticos han llamado Algoritmos Exactos o Algoritmos Aproximados.
Los algoritmos exactos lo que hacen es, de todas las posibles rutas, desprecian la que no les interesan y sólo calculan unas cuentas y de esas se queda con la más corta. Un ejemplo en mi pueblo sería, si tengo que ir de San Antonio a los paradores, la ruta que va por el poli no me molesto en calcularla.
Los algoritmos aproximados se contentan con una ruta muy corta, aunque no se pueda asegurar que no haya una mejor.
Tanto en unos como en otros algoritmos se utilizan varias estrategias. Os cuento una de ellas brevemente y me extiendo en otra, que es a lo que vengo hoy aquí.
Una estrategia que suele dar buenos resultados es “divide y vencerás”. Dividimos el conjunto de ciudades en subconjuntos más pequeños, calculamos la ruta óptima de cada subconjunto y luego las pegamos. Listo.
Otra que me flipa está inspirada en las naturaleza, concretamente en la forma de proceder de las hormigas en la búsqueda de alimentos desde su colonia.
Vamos a intentar explicar de forma intuitiva el hacer de las hormigas para generar el camino más corto entre los nidos y las fuentes de comida.

Las hormigas (exploradoras) se mueven de manera aleatoria alrededor de la colonia. Si encuentran comida, vuelven a la colonia de manera más o menos directa, dejando tras de sí un rastro de feromonas.
En la naturaleza, las feromonas representan un sistema de comunicación química entre animales de una misma especie, informando acerca del estado fisiológico, reproductivo, social, edad, sexo y posible parentesco con el animal emisor.
La fuerza con la que se perciben las feromonas influye en la manera en que reaccionan las hormigas. Estas feromonas son atractivas, por lo que las hormigas que estén cerca tienden a seguirlas (lo que no quiere decir que, a veces, pueden perder el rastro), que les lleva a la fuente de comida encontrada por la exploradora.
Cuando regresan al hormiguero llevando comida, las hormigas refuerzan ese camino liberando más feromonas, haciendo que la ruta quede más marcada. Si existen dos rutas para llegar a la misma fuente de alimentos, la ruta más corta será recorrida por más hormigas que la ruta más larga.
En consecuencia, en la ruta más corta se aumentará en mayor proporción la cantidad de feromonas depositadas y será más atractiva para las siguientes hormigas. Por el contrario, las rutas más largas, al ser menos frecuentadas, pierden feromonas con el tiempo debido a su evaporación y no reciben suficiente refuerzo.
Como resultado, todas las hormigas terminan siguiendo el camino más corto hacia la comida.
De esta forma, aunque una hormiga aislada (exploradora) se mueva esencialmente al azar, cuando actúan en grupo las decisiones cambian. Las hormigas de una misma colonia tienden a elegir los caminos donde perciben una mayor concentración de feromonas. En otras palabras, el comportamiento colectivo da lugar a una estrategia más eficaz que la simple suma de comportamientos individuales.
Y qué ha hecho el mundo matemático, reproducir el comportamiento colectivo de las hormigas con la creación del Algoritmo de Optimización por Colonias de Hormigas (ACO). Es decir, que han tenido que venir las hormigas a enseñarles. Me encanta.
Termino comentado que los problemas en matemáticas se dividen en dos grupos, los tipo P o de “fácil solución” y los tipo NP o de alta complejidad. El problema del viajante es NP y me fascina que las hormigas hayan dado con una solución, aunque sea aproximada. La naturaleza es maravillosa.