Por el interés te quiero Andrés

Estimados lectores, hasta ahora podría decirse que los artículos de “El hater” han sido más o menos curiosos, pero desde luego aportar, lo que es aportar a nuestro día a día, creo que ha sido poco. Hoy, ojalá lo consigamos, viene con vocación de servicio público para intentar meternos en las tripas y comprender un poquito el mundo de las matemáticas financieras. 

Si tienes pasta, estás en el lugar correcto y si no la tienes, pues también, porque seguro que en algún momento la vas a necesitar y tendrás que pedirla. 

En este último caso, te aconsejo que, si la pasta la tienen tus padres, se la pidas a ellos, como mucho te van a solicitar que se la devuelvas cuando puedas y en muchas ocasiones, te perdonarán algo…. o bastante. Pero eso sí, tienen que ver buena actitud por tu parte. Me refiero a que parezca que tienes predisposición para devolverla, aunque ya sabemos que las cosas se complican…

Tengas el dinero o lo necesites, el primer concepto que debes conocer, es el de interés simple. El funcionamiento es el mismo, los que no son iguales son los intereses, ahí está la gracia del negocio bancario. Vamos por partes: 

Supongamos que necesitamos 10.000 € para la reforma de nuestra casa y vamos al banco a solicitar ese dinero. Nos lo aprueban y nos ofrecen un préstamo a 5 años al 5% anual de interés simple con pago por mensualidades. 

La fórmula del interés simple es (el famoso carrete): 

I = C x r x t  

Donde:

I = Intereses que nos cobra el banco por dejarnos el dinero.

C = Capital inicial. El dinero que nos prestan, en este caso 10.000 €.

r = Tipo de interés anual, en este ejemplo 5%, para los cálculos, 0,05. 

t = Tiempo en años, para este préstamo, 5 años. 

Además, llamaremos Cf = C + I, al capital final a devolver, que siempre es el dinero del préstamo más los intereses. 

Vamos a los cálculos: 

I = 10.000 x 0,05 x 5 = 2500 € 

Con esto tendremos que devolverle al banco el dinero que nos ha prestado más los intereses:

Cf = 10.000 + 2500 = 12.500 € 

Como tenemos que devolverlo de forma mensual durante los 5 años, es decir, 60 meses, cada cuota será de:

Cuota mensual = 12.500 : 60 = 208,33 € 

Ahora vamos a ponernos en la posición de una familia que tiene esos 10.000 € y quiere rentabilizarlos. Vamos al banco y le decimos que nos gustaría hacer una inversión segura, sin riesgos y nos ofrecen un depósito a plazo fijo al 3% anual de interés simple con devolución final en un solo pago (normalmente es así).

Los cálculos serían los mismos con una diferencia, el banco siempre va a ofrecer tipos de interés más bajos a los depósitos (metemos dinero) que a los préstamos (sacamos el dinero), por eso ahora nos ofrecen un 3% y antes nos cobraban un 5%. Ahí está la ganancia y además este dinero que nosotros metemos, podría valer para el préstamos anterior, entre otros muchos productos. No me digáis que no son brillantes.

En este caso: 

I = 10.000 x 0,03 x 5 = 1500 € 

Con esto nos devolverán a los cinco años:

Cf = 10.000 + 1500 = 11.500 € 

En fin, que yo os propongo una solución, si tenéis 10.000 € en casa y vuestro primo los necesita para comprarse un coche, prestárselo a 4% de interés simple anual, que os lo devuelva como acordéis en los cinco años, sin ser blandos como vuestros padres y saldréis los dos ganando. 

Este interés simple recibe el nombre de interés “suave” y nos lo vamos a encontrar en préstamos personales o depósitos a plazo fijo, entre otros productos. Lo de “suave” es en comparación con el interés compuesto, que es despiadado con los deudores. 

Podríamos decir que el interés compuesto es un interés simple que se va renovando periodo a periodo, normalmente al año, añadiendo los intereses producidos al capital. Dicho así, parece un poco lioso, así que vamos a verlo con un ejemplo parecido al anterior. 

Volvemos a necesitar los 10.000 € para la reforma de nuestro negocio y el banco nos ofrece un préstamo a 5 años al 5% anual de interés compuesto. 

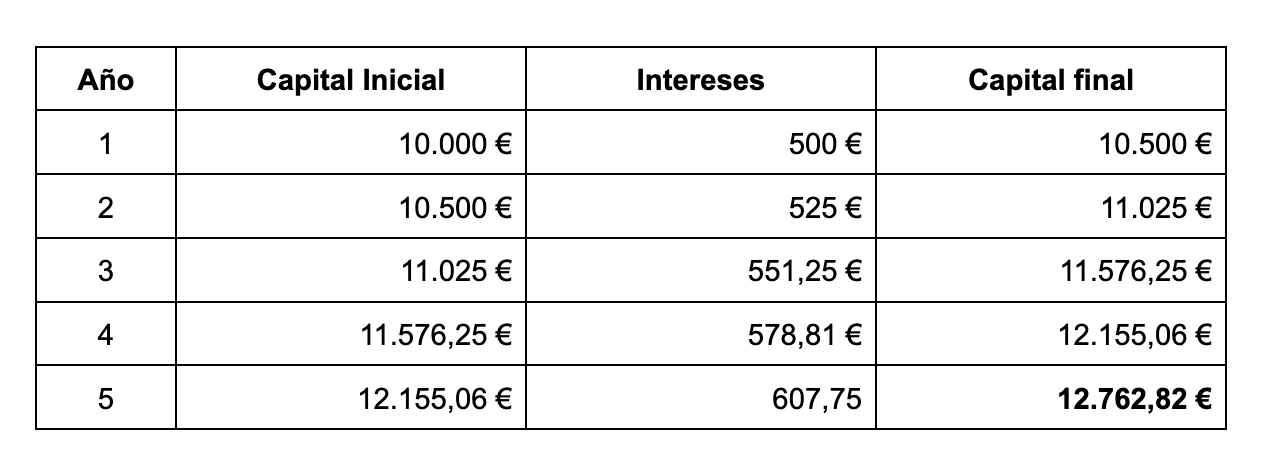
Vamos a calcular los intereses producidos el primer año. 

I1 = C x r x t = 10.000 x 0,05 x 1 = 500 €

C1 = 10.000 + 500 = 10.500 € 

Siendo I1 los intereses producidos el primer año y C1 el capital que tendría que devolver al final de este primer año. 

Sobre esta cantidad vamos a calcular los intereses del segundo año.

I2 = 10.500 x 0,05 x 1 = 525 €

Podéis comprobar que cada año que pasa suben los intereses, os dejo en una tabla el cálculo completo.  

La fórmula para calcular el capital final de una capitalización de interés compuesto es:

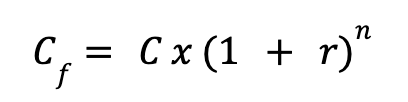
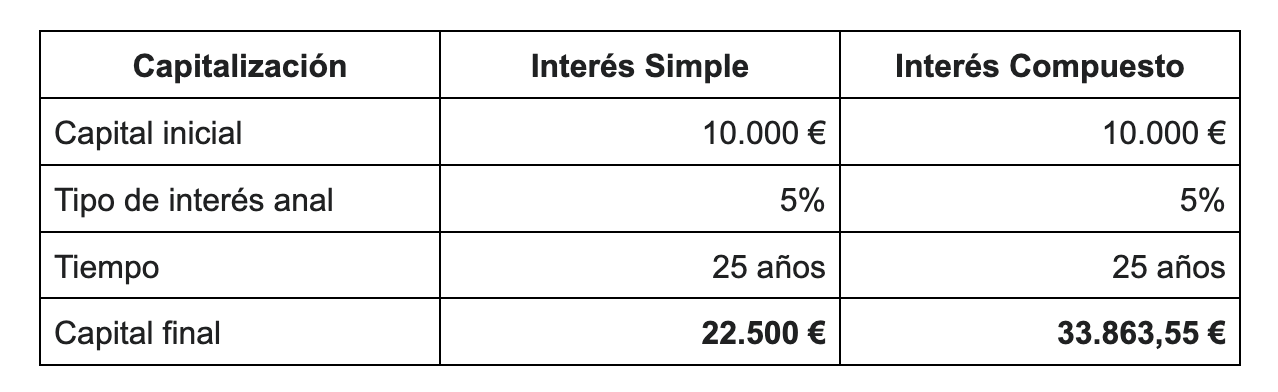
En este caso y a diferencia con el interés simple, tendríamos que devolver 262,82 € más.  Puede parecer poco, pero debemos tener en cuenta que el tiempo es uno de los factores más influyentes en el interés compuesto. 

Imaginemos que el préstamo en lugar de a 5 años, lo ponernos a 25. Veamos la comparativa:

El interés compuesto nos lo vamos a encontrar en tarjetas de crédito (revolving) o en algunas multas impagadas, a las que a la deuda contraída, se les añaden los intereses para calcular los intereses sucesivos. 

Por el contrario, si tenéis pasta, existen planes de pensiones o fondos de jubilación que ofrecen este tipo de interés compuesto. No es mal negocio, pero cuidado porque tributan a hacienda, hay que tenerlo en cuenta. 

No penséis que este tipo de técnica de préstamo de dinero es algo de los últimos siglos, el interés compuesto es tan antiguo como el simple, del que se deriva. Se cree que fueron los sumerios, alrededor de 2400 a. C., los primeros en acuñarlos, recibiendo el nombre de maš, el simple y mašmaš, el compuesto. Pero es en el Derecho Romano, donde al capital compuesto se denomina usurae usurarum, no me digáis que no es una declaración de intenciones.

Pero no nos podemos ir de aquí hoy sin hablar de uno de los productos financieros estrellas, las hipotecas. Quien más quien menos, las sufren o las han sufrido y cómo se está poniendo el precio de la vivienda, cada vez va a ser más difícil acceder a ellas.

Una hipoteca es un préstamo a largo plazo que un banco te da para comprar una vivienda. A cambio, la casa queda como garantía: si no pagas, el banco puede quedarse con ella.

Se devuelve en cuotas mensuales, que incluyen capital (lo que realmente amortizas) e intereses (lo que paga el banco por prestarte el dinero).

El más común para calcularlas es el de método francés, con cuotas fijas donde al principio pagas más intereses y menos capital, pero poco a poco la proporción se invierte.

Básicamente, una hipoteca es la forma de comprar una casa… pero pagándola casi dos veces al final.

Normalmente, aunque las hay de tipo fijo, las hipotecas contratadas son de interés variable, con un índice de referencia, el más usado en España es el Euribor, más un diferencial que negocias con el banco. 

Vamos a poner un ejemplo para que se entienda bien: 

Queremos comprar un piso y además del dinero ahorrado que tenemos, necesitamos 150.000 €. Negociamos con varias entidades bancarias y la que mejores condiciones nos pone es Euribor + 1% de interés a 30 años y decidimos firmar con ella. 

A qué nos referimos con interés variable, a que todos los años en un mes determinado se revisa el Euribor y el valor que tenga ese mes es que que va a servir de referencia para el cálculo de las doce mensualidades siguientes.

Imaginemos que cuando firmamos la hipoteca está el Euribor al 2% anual. Como en el contrato viene que es Euribor + 1%, el primer año vamos a pagar cuotas al 3%. 

La fórmula para el cálculo de la cuota mensual por el métodos francés es: 

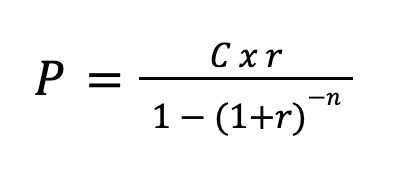
C = Capital inicial, 150.000 €. 

r = Tasa mensual, 0,03/12 = 0,025 

n = Número de pagos, 30 x 12 = 360 mensualidades.

P = Pago de cada cuota mensual. 632,41 €

La distribución de pago de intereses y amortización el primer años es la siguiente:

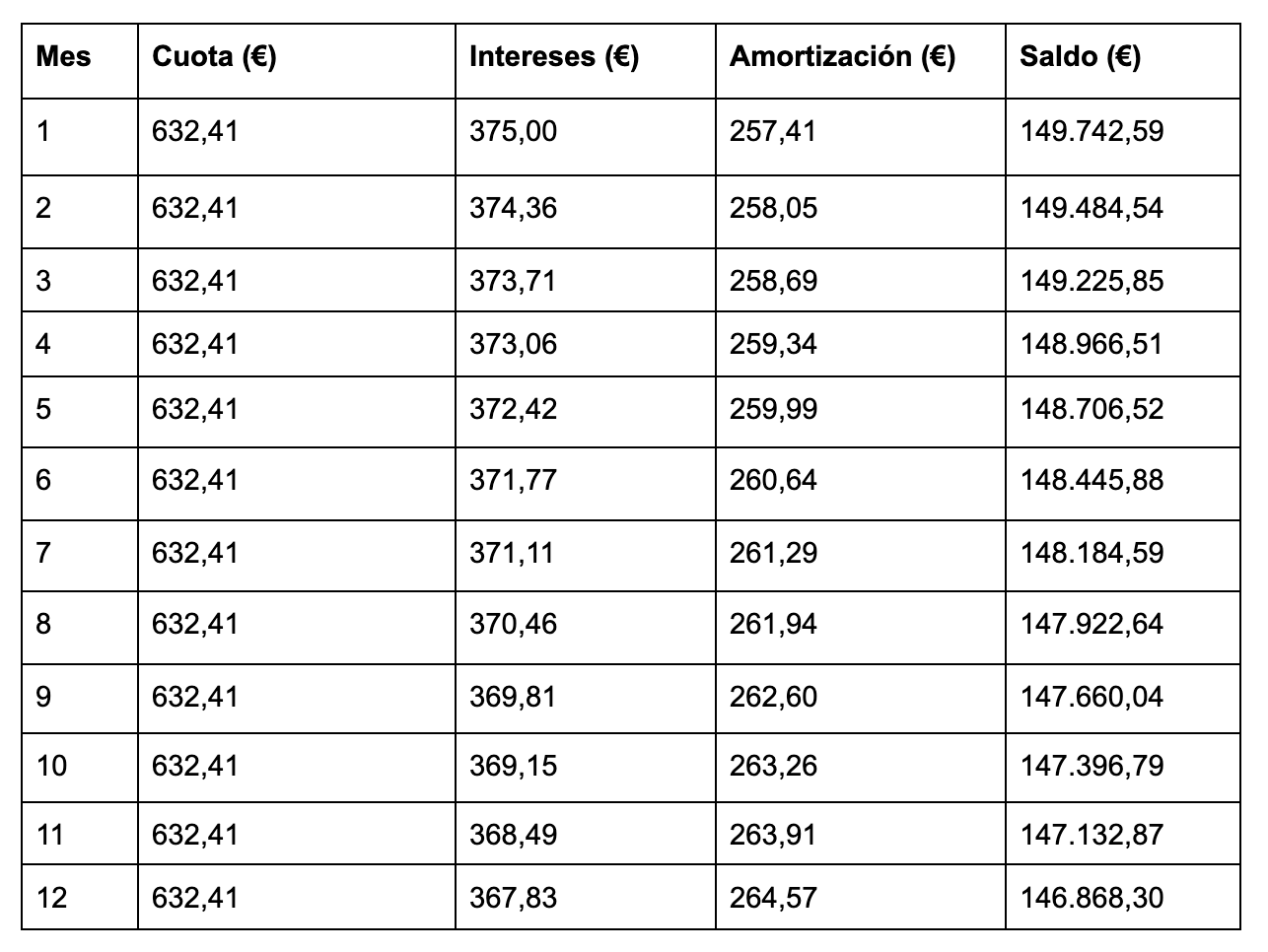
En total, el primer año habremos pagado 4.500,07 € en intereses y se habrá amortizado 3.137,9 € del capital, por lo que nos quedan por amortizar 146.868,30 €.

Se revisa de nuevo el Euribor y resulta que está al 2,5%, ha subido 0,5 € respecto al año anterior. ¿Cómo afecta esto a nuestra hipoteca? Durante el siguiente año se vuelve a calcular la cuota sobre el capital pendiente a amortizar, en nuestro caso 146.868,30 €, quedando el cuadro de amortización así:

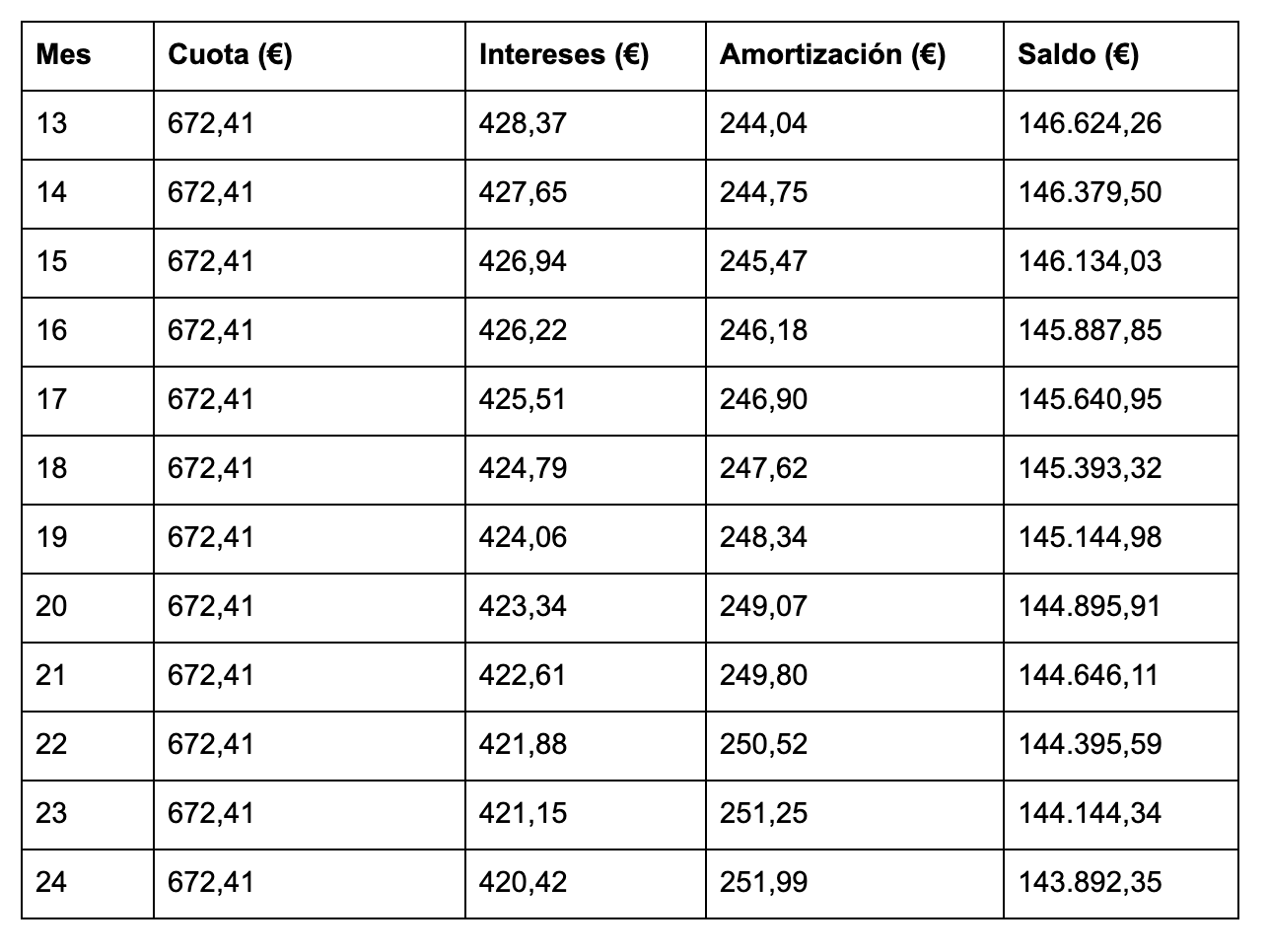
Es decir ese 0,5% más de Euribor significa 40 € más en nuestra hipoteca. 

Para finalizar vamos a calcular cuántas veces vamos a pagar la casa. Pogámonos en una situación optimista, es decir, que el Euribor no cambiase en 30 años, algo inverosímil, pero para hacernos una idea, siempre al 3%.

Cuota mensual: 632,41 €

Mensualidades: 360 

Total a pagar: 632,41 x 36 = 227.667, 60 € 

En fin, la banca siempre gana y eso que no os he hablado de las comisiones, pero ahí no hay matemáticas, ahí hay mucha cara dura. 

Adiós Andresillos!!