Pitágoras: El hombre que nos arruinó la vida con los triángulos

“Dichoso Pitágoras, aparece por todos los lados, qué bien estaríamos si no hubiera existido”, comentan mis alumnos cuando alargando alguna línea o trazando una perpendicular aparece de la nada algún triángulo rectángulo. Y no les falta razón, qué tranquilos estaríamos todos…

Hoy va la cosa, como ya os podréis imaginar, de este personaje que, aunque no nos guste, es más conocido que Taylor Swift, con algún ‘like’ menos en redes sociales ,eso sí. De él y del teorema que lleva su nombre. 

Sabemos que nació en la isla de Samos, en el Mar Egeo, sobre el año 570 a. C. y que después de picotear en varios lugares, se estableció en la Magna Grecia, lo que es ahora el sur de Italia, muriendo alrededor del año 490 a.C. Ochenta añitos vivió el colega, no está nada mal para la época. 

Procedía de familia acomodada, lo que le facilitó estudiar gran variedad de disciplinas como poesía, música, matemáticas, astronomía y filosofía. Gracias a estos conocimientos fundó una escuela de pensamiento que combinaba aspectos filosóficos, místicos y científicos: La Escuela Pitagórica. 

La idea central del pensamiento pitagórico fue “los números como esencia de todo”, centrando su estudio en las matemáticas y la geometría.

En las investigaciones sobre él, es difícil distinguir qué ideas son propias y cuáles de sus seguidores, por un lado, no dejó material escrito sobre su trabajo y por otro, los pitagóricos lo citaban sistemáticamente como fuente de autoridad para dar más peso a sus propias ideas: es posible que ni siquiera el famoso teorema de Pitágoras fuese formulado directamente por él. 

Y dicho esto, pongámonos en posición, se define triángulo rectángulo como el triángulo que tiene un ángulo recto, es decir, mide 90 grados. Recibe el nombre de hipotenusa el lado de mayor longitud, opuesto al ángulo recto y catetos los lados que forman dicho ángulo. 

Y qué dice el manido Teorema de Pitágoras:

En todo triángulo rectángulo, el cuadrado de la hipotenusa es igual a la suma de los cuadrados de los catetos. 

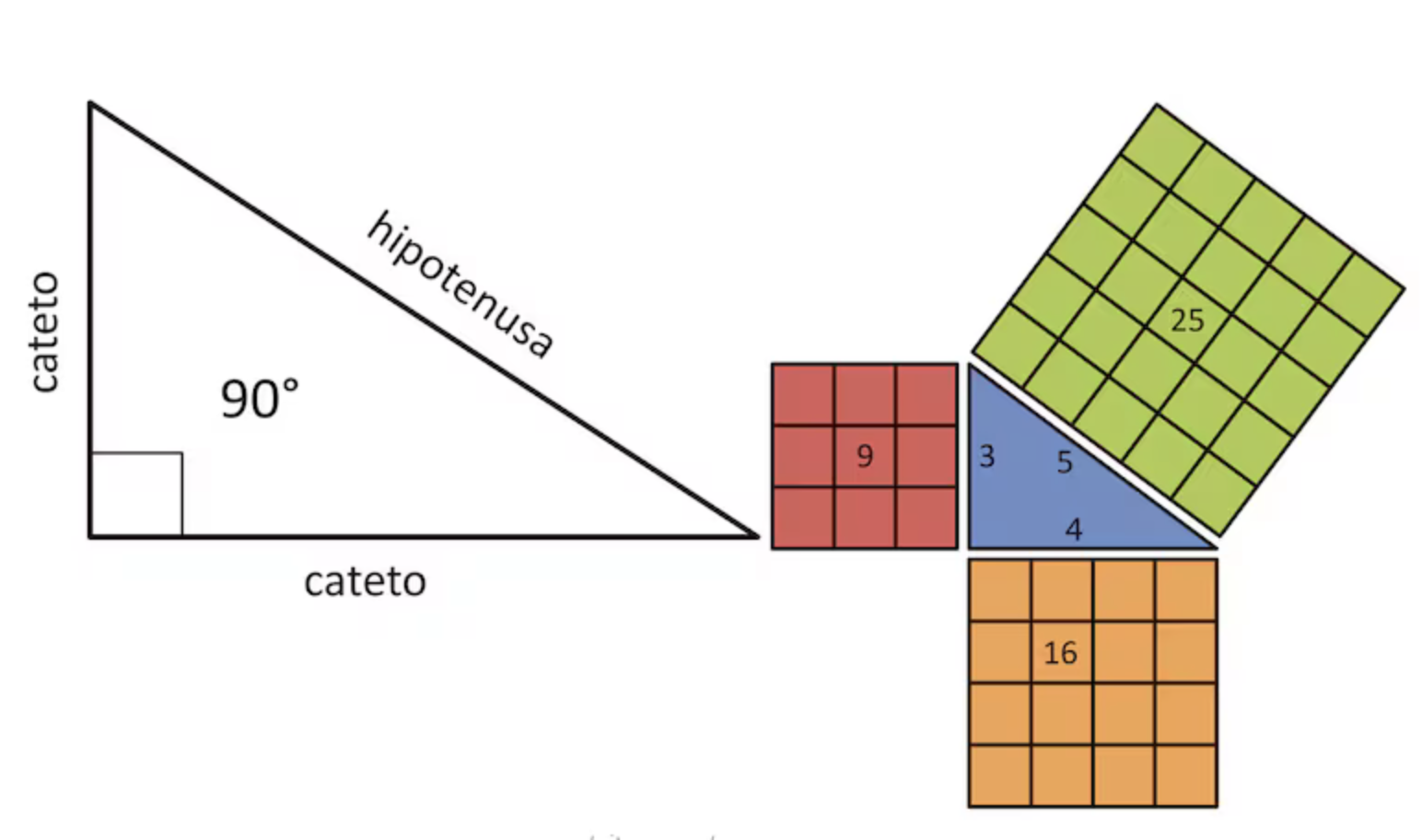
Geométricamente se puede interpretar como que el área de un cuadrado cuya longitud del lado es igual a la de la hipotenusa de nuestro triángulo, es igual a la suma de las áreas de los cuadrados cuyos lados miden lo mismo que los dos catetos del mismo triángulo. Lo que tenéis en el dibujo de arriba. 

Pero creéis que fue Pitágoras el primero en darse cuenta de esta relación entre los lados de un triángulo rectángulo. No, mucho antes, en la antigua Babilonia ya la habían descubierto, como prueba de ello está la Plimpton 322, una tableta de arcilla que data entre 1822 y 1766 a. C. con la existencia en escritura cuneiforme de varias ternas pitagóricas, de las que luego hablaremos. Después, esta relación, se usaría en Mesopotamia y Egipto.   

Y entonces, ¿por qué recibe este nombre? Posiblemente porque fuese la escuela pitagórica la primera en demostrarlo, aunque no hay certeza absoluta.

Demostraciones distintas del Teorema de Pitágoras hay a cascoporro, algunos autores las cifran en más de mil, que digo yo que una vez demostrado, para qué molestarse, pero ya sabéis, los matemáticos. El autor estadounidense E. S. Loomis recuperó 367 demostraciones diferentes en su libro de 1927 The Pythagorean Proposition. No tendría otra cosa que hacer este hombre.  

Entre los reputados autores que han logrado demostrarlo está Euclides, Pappus de Alejandría o el mismísimo Leonardo Da Vinci, pero si yo me tuviera que quedar con alguna, por fácil, me quedaría con Garfield, el gato, noooo, otro. 

Os hablaba antes de la Plimpton 322 en Babilonia, donde aparecían ternas pitagóricas. Qué son ternas pitagóricas, diréis. Los Triples Pitagóricos o Ternas Pitagóricas son un conjunto ordenado de tres números enteros (sin decimales) positivos que cumplen el teorema de Pitágoras. 

La terna pitagórica por excelencia es (3,4,5), probemos:

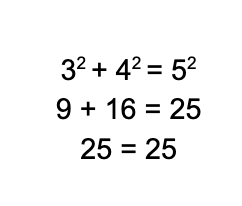
Además existen fórmulas para calcular infinitas ternas pitagóricas, imaginaos lo que supone esto para el mundo matemático. La más sencilla dice que si multiplicas una terna pitagórica por cualquier número natural, el resultado también es una terna pitagórica. Por ejemplo: 

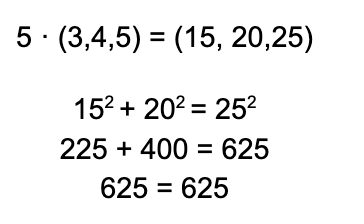
Y además estas ternas son útiles y muy útiles, cualquiera que quiera trazar sobre el terreno un ángulo de 90º solo tiene que tomar una tiza y rayar 15 cm en una dirección, 20 cm en una dirección que más o menos sea perpendicular, es decir, que forme un ángulo recto y si los extremos de esos lados que ha pintado se unen en un segmento que mide 25 cm, el ángulo que han pintado es de 90º. Te lo juro por Pitágoras. 

Y con esto ya entramos en terreno de Tales y no nos vamos a meter ahí, eso lo dejamos para otro día. 

¡Adiós pitagorines!