
Cinco y cinco cero y me llevo una

No sé si recordáis cuál fue vuestro primer trabajo. En mi caso no soy capaz de ubicarlo en el tiempo concretamente, de hecho creo que incluso tuve dos simultáneos, monaguillo y reponedor en la tienda de mi tío Domingo. “Armería y alimentación Domingo Lorenzo”, ya sabéis, esas tiendas que había en los pueblos en las que se mezclaba género tan variopinto como alimentación, cordelería o armas de caza, en este caso. Me estoy retrotrayendo a los últimos años de la década de los ochenta del siglo pasado, que ya ha llovido.
Mi contrato en la tienda por aquella época era a tiempo parcial, los sábados por la mañana, ampliable en vacaciones a algún día de diario, también de mañana, que por la tarde tocaba la piscina del pueblo.
Entonces no existían las básculas electrónicas con impresión de tickets, ese fue el siguiente paso, la cuenta de la compra se hacía a mano. Se colocaba todo en el mostrador, en primer lugar se pesaba lo que iba a granel (lentejas, naranjas, puerros..) y una a una se multiplicaba ese peso (masa) por el precio del kg. Hechas estas operaciones se sumaba todo (lo pesado más los productos con precio unitario) en una cuenta larguísima que en muchas ocasiones superaba los veinte sumandos.
Recuerdo perfectamente a mi tío realizando estas cuentas en papel de estraza con su boli bic llevándose tres o cuatro sin equivocarse ni una cifra. Luego rompía el papel y se lo daba a la clienta, casi siempre clientas.
A veces, alguna le decía que no lo quería y ese era mi momento, uno que ya tenía inquietudes aritméticas, repasa la cuenta con todo ahínco a ver si había algún error, pero nada, una y otra vez todo cuadraba.
Hoy tocan sumas queridos lectores, concretamente algunos de los algoritmos que se utilizan para realizarlas, esos que aprendimos y se siguen aprendiendo en los colegios, deteniéndonos en su explicación matemática.
Recordáis el algoritmo con el que aprendisteis, yo con el tradicional, el de llevarse una… Vamos con él.
Hace poco hablamos en el artículo Dorothea y el sistema de numeración hindú que el sistema de numeración decimal es un sistema posicional aditivo, posicional porque las cifras tienen distinto valor dependiendo de la posición que ocupan y aditivo porque para calcular el total del número hay que sumar los valores de sus cifras.
Recordemos un ejemplo sencillo:
1.245,37 = 1000 + 200 + 40 + 5 + 0,3 + 0,07 = 1 x 1000 + 2 x 100 + 4 x 10 + 5 x 1 + 3 x 0,1 + 2 x 0,01
Estas posiciones tienen nombre y en nuestro caso:
El 1 ocupa la posición de las unidades de millar (UM), el 2 ocupa la posición de las centenas (C), el 4 las decenas (D), el 5 las unidades (U), el 3 las centésimas (d) y el 7 las centésimas (c). Seguro que lo recordáis.
Para sumar por el método tradicional, alineamos los números verticalmente, asegurándonos de que las unidades estén debajo de las unidades, las decenas debajo de las decenas, y así sucesivamente para todas las posiciones.
Por ejemplo 347 + 236 + 59
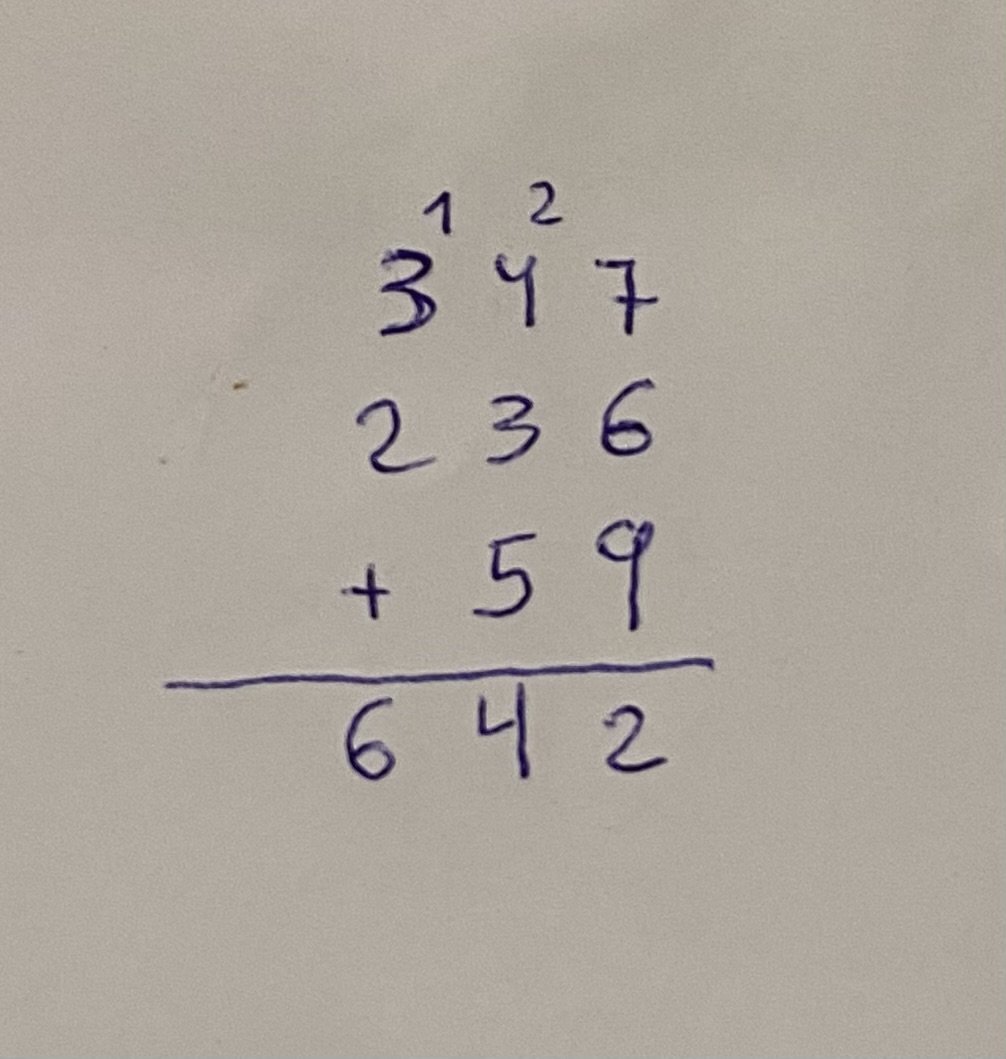
Se comienza a sumar las cifras que se encuentran en la posición de menor valor, en este caso sumamos las unidades.
7 + 6 + 9 = 22 = 20 + 2 = 2 D + 2 U
Colocamos en la vertical de las unidades debajo de la línea horizontal el 2 y decimos “me llevo 2” que traducido al lenguaje matemático quiere decir que esos 20, esas 2 decenas las voy a sumar al resto de decenas que tenemos. Normalmente ese 2 lo solemos poner arriba en pequeñito para que no se nos olvide.
El siguiente paso es sumar las decenas:
5 + 3 + 4 + 2 “que me llevo” = 14 (cuidado, 14 decenas) = 1 C + 4 D
Volvemos a colocar, en este caso el 4, debajo de la línea horizontal en la posición de las decenas y ahora “me llevo 1”.
De nuevo escribimos el 1 en pequeñito arriba en la vertical de las centenas y las sumamos:
2 + 3 + 1 “que me llevo” = 6
Colocamos el 6 debajo de la línea horizontal en la posición de las centenas y hemos terminado.
Resultado 6 C + 4 D + 2 U = 642
Aunque es el algoritmo más usual, no es el único.
Os presento el algoritmo de “la suma de izquierda a derecha”, “suma de alta a baja” o “suma comenzando por los dígitos más significativos” aunque no tiene un nombre ampliamente reconocido.
Realicemos la misma suma que antes, 347 + 236 + 59
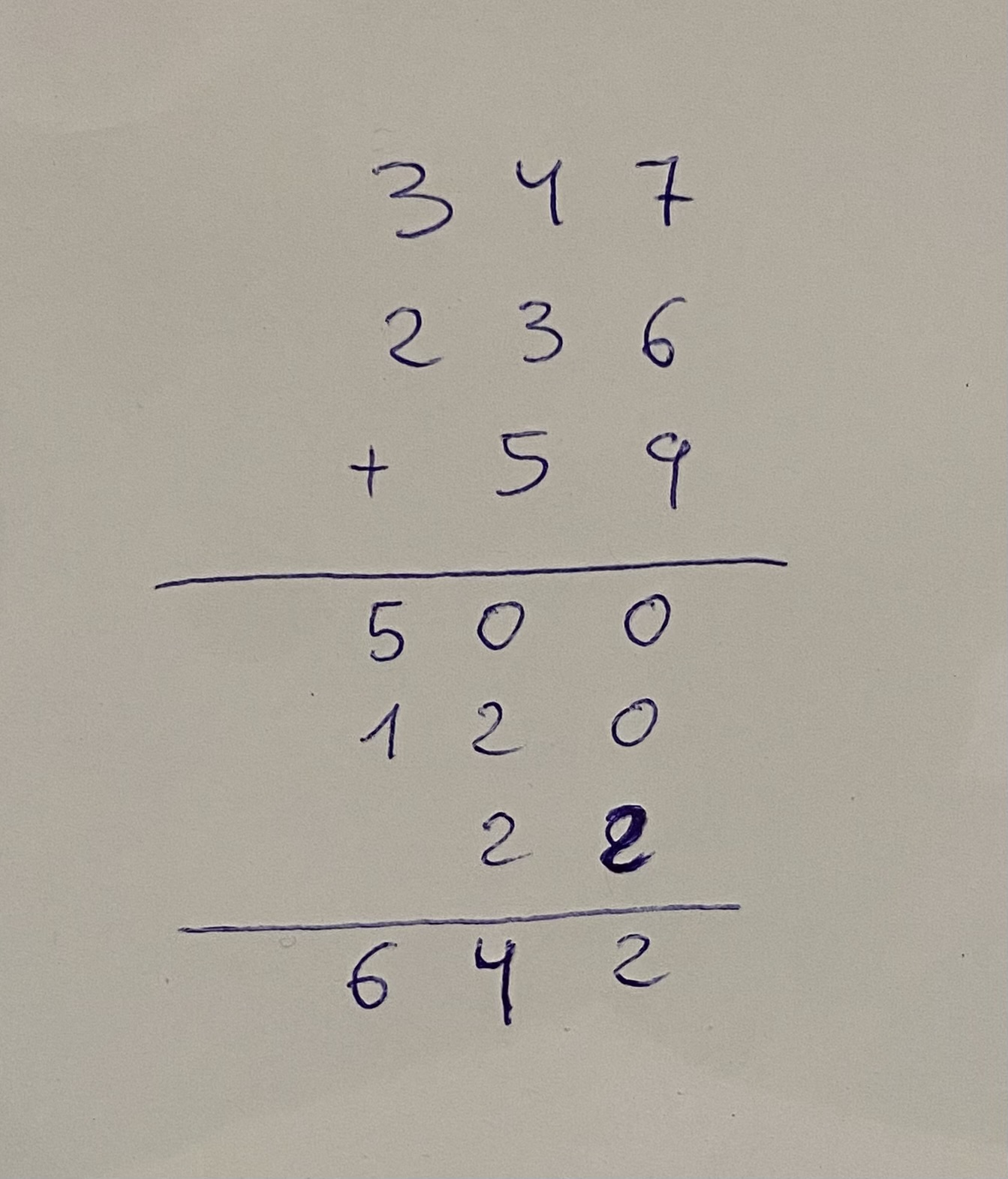
En este caso comenzamos sumando por la izquierda, como indica su nombre. En nuestro ejemplo las centenas:
3 + 2 = 5 C = 500
Colocamos el 500 debajo de la línea horizontal.
En segundo lugar sumamos las decenas:
4 + 3 + 5 = 12 D= 120
Colocamos el 120 debajo del 500
Por último sumamos las unidades:
7 + 6 + 9 = 22
Ahora colocamos el 22 debajo del 120 y sumamos de nuevo de izquierda a derecha.
5 + 1 = 6 C + 2 + 2 = 4 D + 2 U = 642
Y otro más, la suma por el método ABN “Algoritmo Basado en Números” que desarrolló el maestro y doctor en Filosofía y Ciencias de la Educación español Jaime Martínez Montero. El método ABN se centra en la comprensión profunda del valor posicional de los números y permite a los estudiantes manipularlos de manera flexible y significativa.
Veamos un ejemplo:
347 + 236
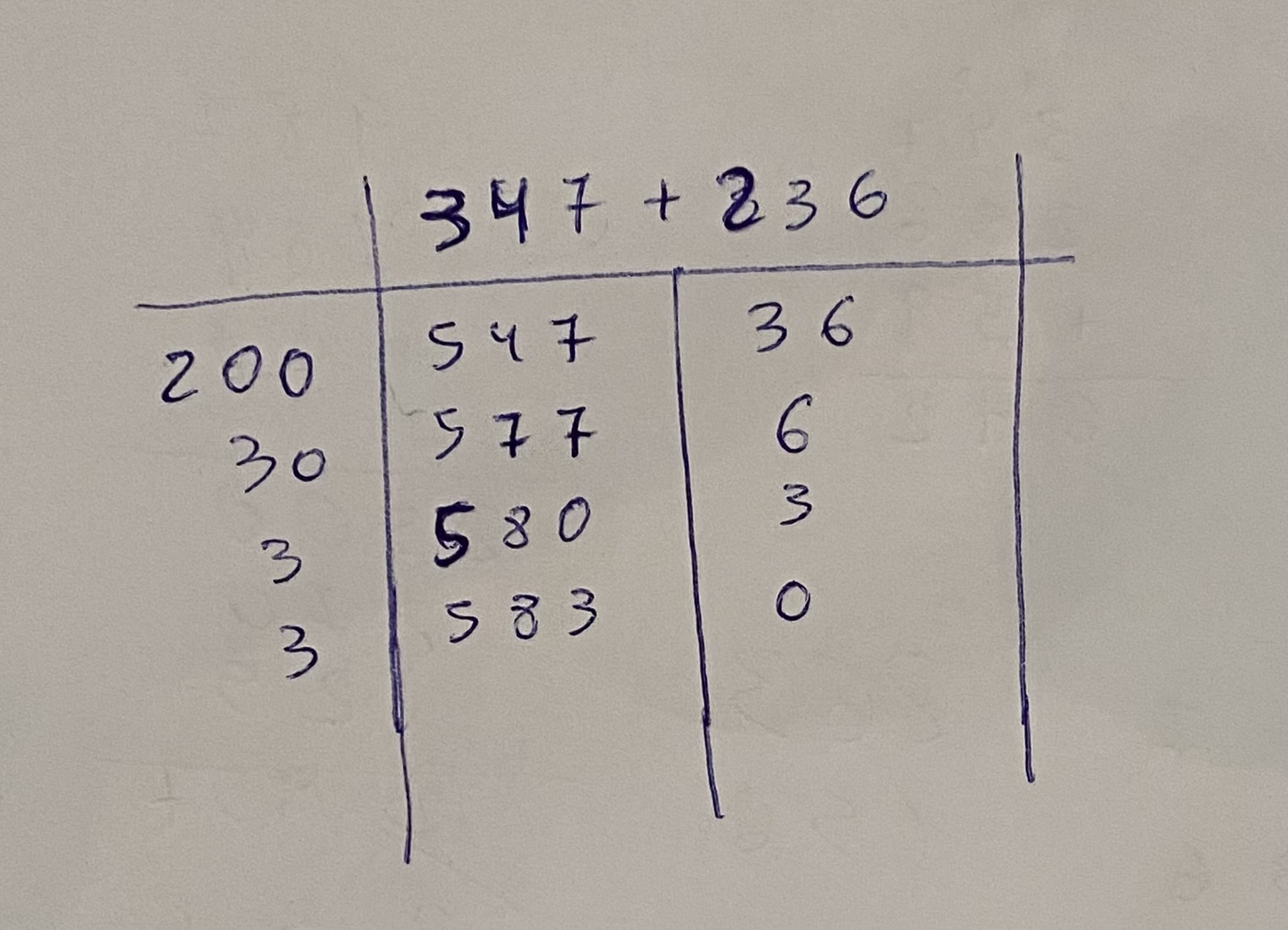
Esto que veis es la rejilla de ABN y consiste básicamente en pasar cantidades, cada uno las que quiera y las veces que le convenga, de un número a otro. Normalmente se hace del pequeño al mayor, pero no es obligatorio.
Os cuento como lo he hecho:
En primer lugar le paso 200 del 236 al 347. Coloco el 200 en la columna de la izquierda, le sumo 200 al 347, que es una suma fácil (200 + 347 = 547) lo ponemos en la columna central y le quito al 236 el 200 que he pasado, quedándome 36 en la columna de la derecha.
Ahora le paso 30 del 36 al 547. Escribimos 30 en la columna de la izquierda, sumamos 547 + 30 = 577 y del 36 ya sólo nos quedan 6 al pasarle 30.
En ABN las cifras que suman 10 se llaman “amigas”, así el 1 es “amigo” del 9, el 2 es “amigo” del 8…
Como me quedan 6 y las unidades del 577 son 7, un recurso muy utilizado en este método es trabajar con el “amigo” del 7 que es el 3.
De los 6 que nos quedan pasamos 3, que lo ponemos en la columna de la izquierda, sumanos 3 + 577 = 580 que va a la columna central y nos quedan 3 a la derecha.
Terminamos sumando 3 + 580 = 583 y hemos terminado.
Qué os parece, tenéis predilección por alguno de ellos. Supongo que para gustos los colores.
Desde el punto de vista educativo, sinceramente creo que no hay un método mejor que otro a la hora de enseñar a los niños, pero aquí entra en juego la importancia de los proyectos educativos de los centros, que son los que deben marcar la línea de trabajo con el alumnado. Lo que no puede pasar es que un docente comience a enseñarles con un algoritmo y en cursos sucesivos les cambien a otro, porque ahí es donde los lían.
Termino comentando que esta semana nos dejó mi tío, se fue a realizar sumas interminables a otro sitio, lo mismo ahora las hace “de izquierda a derecha” o por el método ABN. Da igual, lo que estoy seguro es que seguirá sin equivocarse, porque para eso tenía un don. Vaya dedicado este humilde artículo a él.
























