El capicúa de un número

Este hater normalmente la tiene tomada con los matemáticos, pero hoy queridos lectores seguro que alguno de vosotros, sin serlo, también os vais a llevar lo vuestro porque sé que más de uno o de una le pierden los números a los que le vamos a dedicar el artículo. 

Un número capicúa es aquél que leído de izquierda a derecha se lee igual que de derecha a izquierda.

El número 12.321 sería un ejemplo de número capicúa de cinco cifras. Y qué pasa, que sé que a muchos de vosotros os pierden este tipo de números y si pasáis por una administración de lotería y véis ese 12.321 para el sorteo de Navidad no os podéis ir sin comprarlo. Y me parece una actitud muy razonable, porque raro es el año que no cae entre los números premiados un capicúa (léase la ironía).

A otros muchos les llama la atención las matrículas que cumplen esta secuencia simétrica y rápidamente dejan todo lo que tienen entre manos para concentrar sus cinco sentidos en esta particularidad, algún día os multan y no será porque no os lo estoy advirtiendo. 

Estos numeritos que tanta atracción producen también reciben el nombre de palíndromos, en clara alusión a las palabras se leen igual de izquierda a derecha que de derecha a izquierda, también llamadas capicúas. En fin, tanto monta…

Los palíndromos o capicúas ya aparecen en la obra Ganatasarasamgraha, un compendio matemático del año 850 del autor indio Mahaviracharya, en el cual se hablaba del número que comienza por el uno aumentando progresivamente hasta el seis y luego disminuyendo del mismo modo, refiriéndose claramente al 12.345.654.321. Y posiblemente este tipo de números capicúas, los que empiezan por uno, van aumentando de uno en uno y luego disminuyen con la misma cadencia, sean los que cumplen las propiedades más curiosas.

La primera que nos encontramos es que pueden obtenerse como el cuadrado de números formados por unos, fijaos:

1 x 1 = 1

11 x 11 = 121

111 x 111 = 12.321

1.111 x 1.111 = 1.234.321

11.111 x 11.111 = 123.454.321

111.111 x 111.111 = 12.345.654.321

Y podéis seguir hasta llegar al resultado 12.345.678.987.654.321

Pero no se queda ahí la cosa, además si sumamos las cifras de estos números, su resultado es un cuadrado perfecto. 

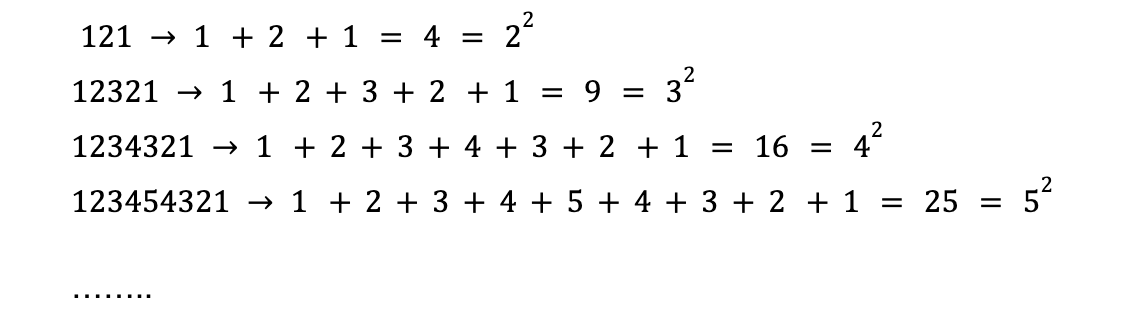
Es más, podemos rizar el rizo y estos palíndromos los podemos obtener como resultado de estas expresiones tan sorprendentes.  

La pregunta que me hago es: ¿quién se enredará a ésto?

Pero a los que el mundo matemático le ha dedicado más tiempo y se lo siguen dedicando es a los “capicúa de un número”.

Definamos estos números, son aquellos que se obtienen como sumas reiteradas de un número y su simétrico (dándole la vuelta) hasta llegar a uno capicúa. 

Calculemos algunos de ellos para que se entienda bien. 

Capicúa del número 17

17 + 71 = 88, capicúa, lo hemos conseguido en una iteración.

Capicúa del 67 

67 + 76 = 143 

Se sigue con el mismo proceso con 143 

143 + 341 = 484, capicúa, en este caso se ha conseguido en dos iteraciones.

Probemos con el 95

95 + 59 = 154

154 + 451 = 605

605 + 506 = 1.111 capicúa en tres iteraciones.

Yo creo que ya vais viendo cómo va el proceso, ¿verdad? 

No os recomiendo que lo intentéis con el 89, que se llega a su capicúa en 24 iteraciones siendo éste el 8.813.200.023.188.

Os dejo un gráfico del cálculo de los números capicúas de los cien primeros números.

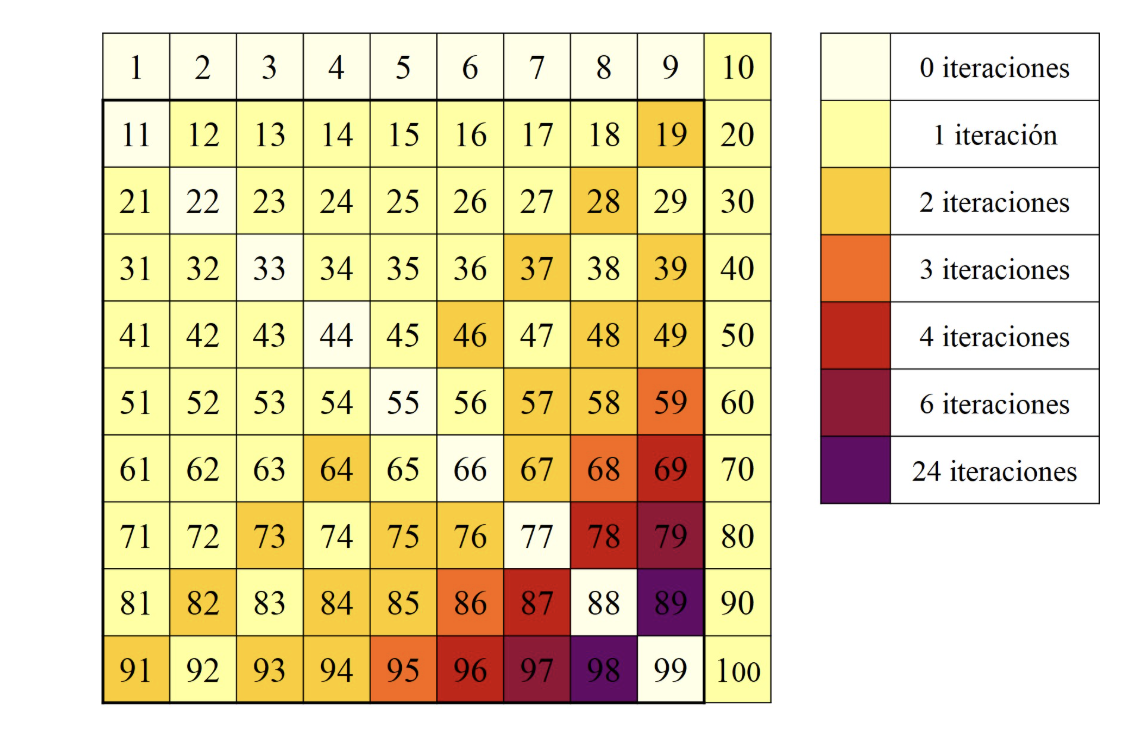
La pregunta que seguro que os estáis haciendo ahora es: ¿todos los números tienen su capicúa?

Según este gráfico los cien primeros números sí, pero lo cierto es que hay números que no se sabe ni que sí, ni que no, es decir, que alguien se ha puesto a hacer iteraciones, una, otra, otra… y nada, no llega a un número capicúa. Y claro, todo el mundo sabe el tiempo en el que vivimos, la era de la informática, la computación, los grandes servidores…. quiero decir con esto que hay números, con la ayuda de los ordenadores, a los que se le habrán aplicado tropecientosmilmillones de iteraciones y no ha habido suerte. 

El más pequeño de todos los que no lo cumplen es el 196, este numerillo aparentemente inocente, par, múltiplo de 4 y de 7, nada de nada… de momento. Un tal Romain Dolbeau, con su programa “p196_mpi” ha conseguido más de un billón de iteraciones y no ha llegado a su deseado palíndromo. 

De hecho, a estos números a los que no se llega a conocer su capicúa se les ha bautizado con el nombre de “números de Lychrel”, en honor a la novia de un matemático, Wade VanLandingham, que trabajaba en este tema. ¡Eso es amor!

La sucesión de los primeros números de Lychrel está formada por 196, 295, 394, 493, 592, 689, 691, 788, 790, 879, 887, 978, 986, 1.495… 

Es el momento de realizar las iteraciones del 196.

196 + 691 = 887

Fijaos arriba, 887 es otro número de Lychrel. Si nos detenemos un momento aquí y lo pensamos un poquito, todos los números que nos vayan saliendo en las iteraciones de un número de Lychrel serán también números de Lychrel, por lo que podríamos decir que hay números de Lychrel de primera y de segunda. Así es, los números de Lychrel se dividen en dos tipos, las “semillas”, que son los más pequeños que generan un “hilo” de iteraciones, como el número 196, o los “familiares”, que son aquellos que forman parte de un hilo generado por una “semilla”, como 887 que está en el hilo del 196, o aquellos que engendran el mismo hilo de que una “semilla”, como el número 295 (ya que, 295 + 592 = 887, que está en el hilo del 196.

De esta manera, en realidad, para realizar el estudio de estos números simplemente es necesario estudiar las “semillas”, ya que los “familiares” tienen el mismo comportamiento, simplificando mucho el trabajo, de hecho solamente hay cuatro “semillas” menores que 10.000, el 196, 879, 1.997 y 7.059, aunque amigos, a partir de 10.000, hay muchas más “semillas”, el problema se hace más grande.

Y claro, el mundo matemático ya tiene aquí un problema abierto y ya sabéis que no hay algo más que le ponga a este colectivo que le dejen un caramelito como este…

Para terminar me gustaría mostraros hasta dónde puede llegar el frikismo palindrómico, el mayor número de iteraciones que se necesitan para obtener un número capicúa que se ha encontrado mediante este proceso, es de 261, que convierten el número 1.186.060.307.891.929.990 en un número capicúa de 119 dígitos. 

Y como dice mi amigo Fran, “¿y esto qué produce?” Al menos, amigos,  comprad ese número de lotería, que este año seguro que toca.