
Los números imaginarios

Imaginemos que lanzamos una pelota hacia arriba,en vertical. Debido a la fuerza de la gravedad, llegará un momento en el cual la pelota comenzará a bajar hasta llegar de nuevo al mismo sitio. Vamos a considerar el lugar desde donde sale y al que que llega la pelota altura 0.
Podríamos ajustar la altura a la que se encuentra la pelota a lo largo del tiempo por medio de la función:
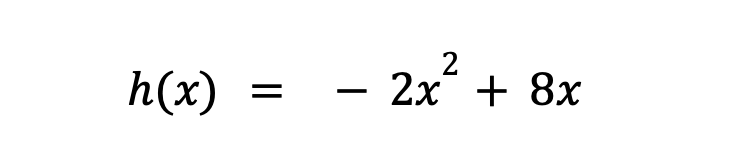
donde h(x) nos indica la altura a la que se encuentra la pelota y x el tiempo transcurrido en segundos.
Vamos a probar a ver cómo se comporta la pelota.
En x = 0, es decir, cuando lanzamos la pelota, la altura se calcula sustituyendo en h(x) la x por 0.
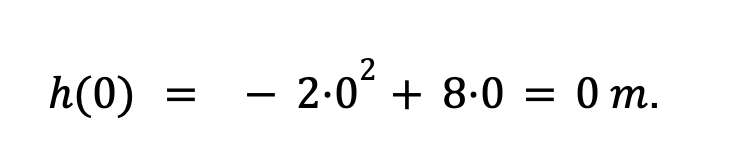
Es decir, al lanzarla, la pelota se encuentra a cero metros de altura.
Veamos qué pasa cuando ha transcurrido un segundo desde que se lanzó, en este caso sustituimos x por 1 seg.
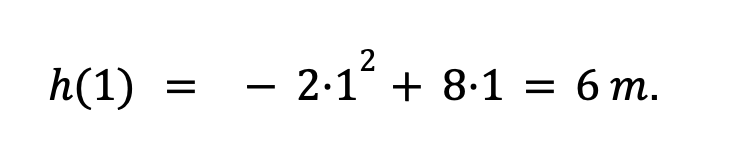
La pelota se encuentra a una altura 6 m. más alta que el lugar desde donde partió.
Si seguimos calculado a los 2, 3, 4… segundos, los resultado son los siguientes:

Observando la tabla parece ser que la pelota sube al principio muy rápido, a los 2 segundos tiene toda la pinta de alcanzar la altura máxima y a partir de ahí baja hasta llegar al lugar inicial a los 4 segundos.
Con la ayuda de GeoGebra lo representamos y efectivamente, lo que ocurre es eso.
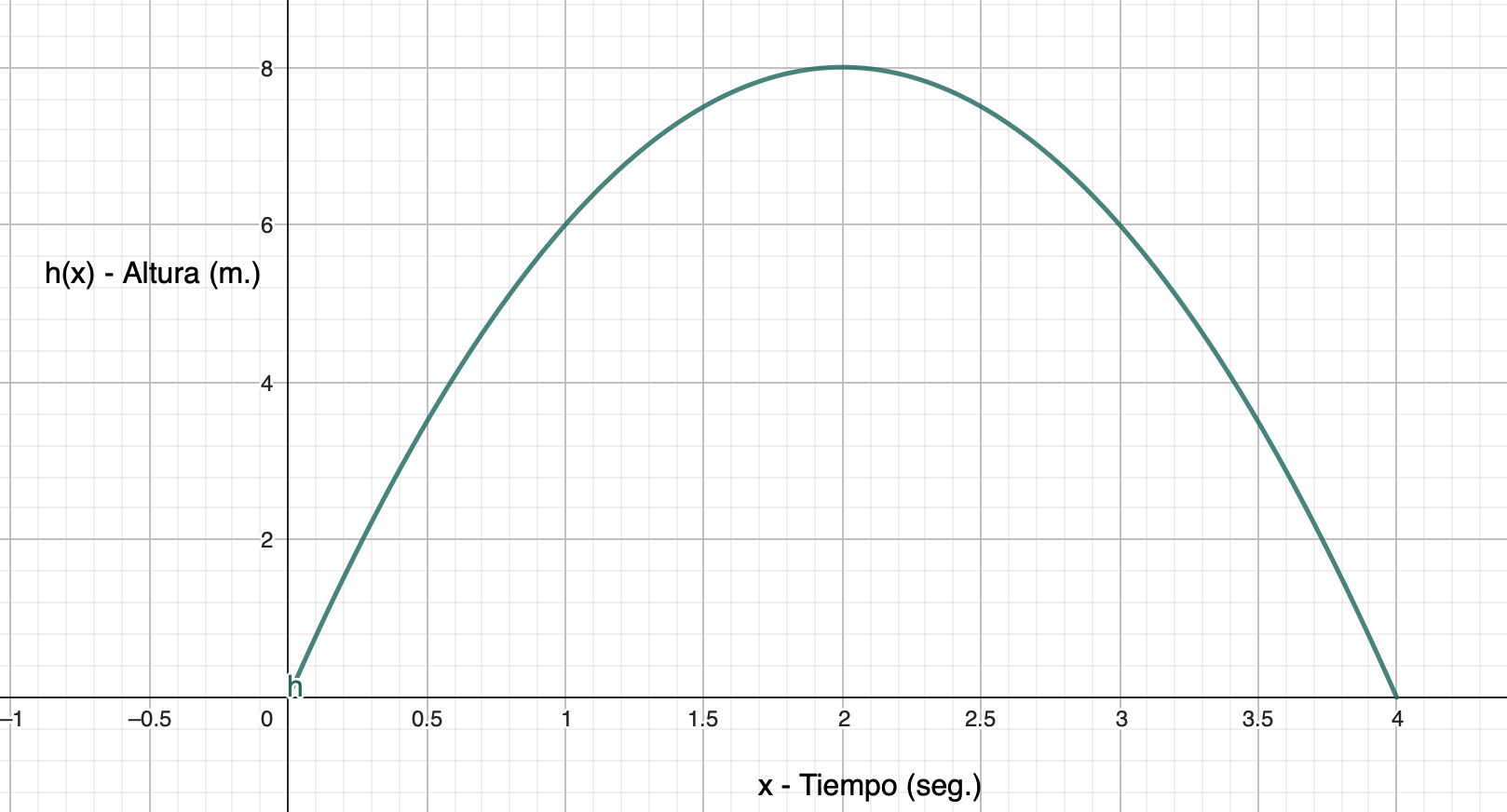
Si no hubiésemos representado la altura de la pelota en función del tiempo que pasa desde que se lanzó y nos hiciésemos la siguiente pregunta: ¿En qué momento la pelota alcanza los 7 metros de altura?
Creo que todos convendréis conmigo en que habrá que ver cuando la altura es igual a 7 m, es decir, cuando h(x) = 7.
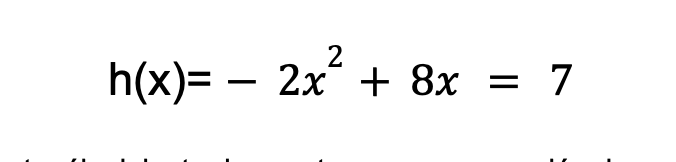
¿Os suena? Eso que tenéis delante de vosotros es una ecuación de segundo grado de toda la vida. Acabamos de dar el salto desde las funciones a las ecuaciones, en matemáticas, del análisis al álgebra.
Os dejo aquí, para refrescaros la memoria, la solución de la ecuación de segundo grado:
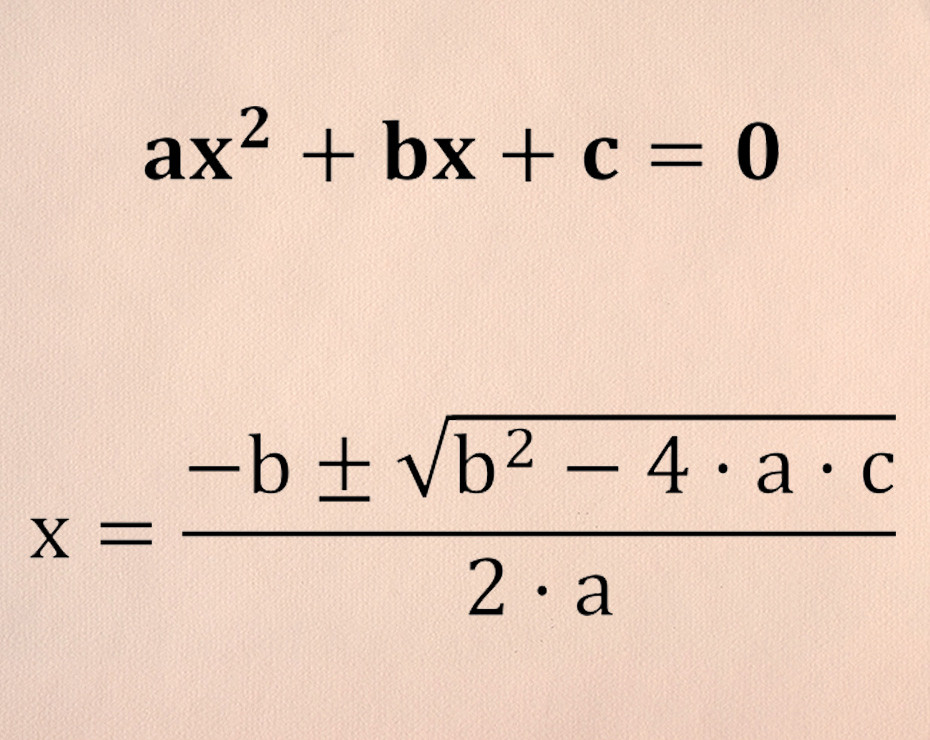
Donde a, b y c son los coeficientes de la ecuación.
Resolvamos la nuestra:
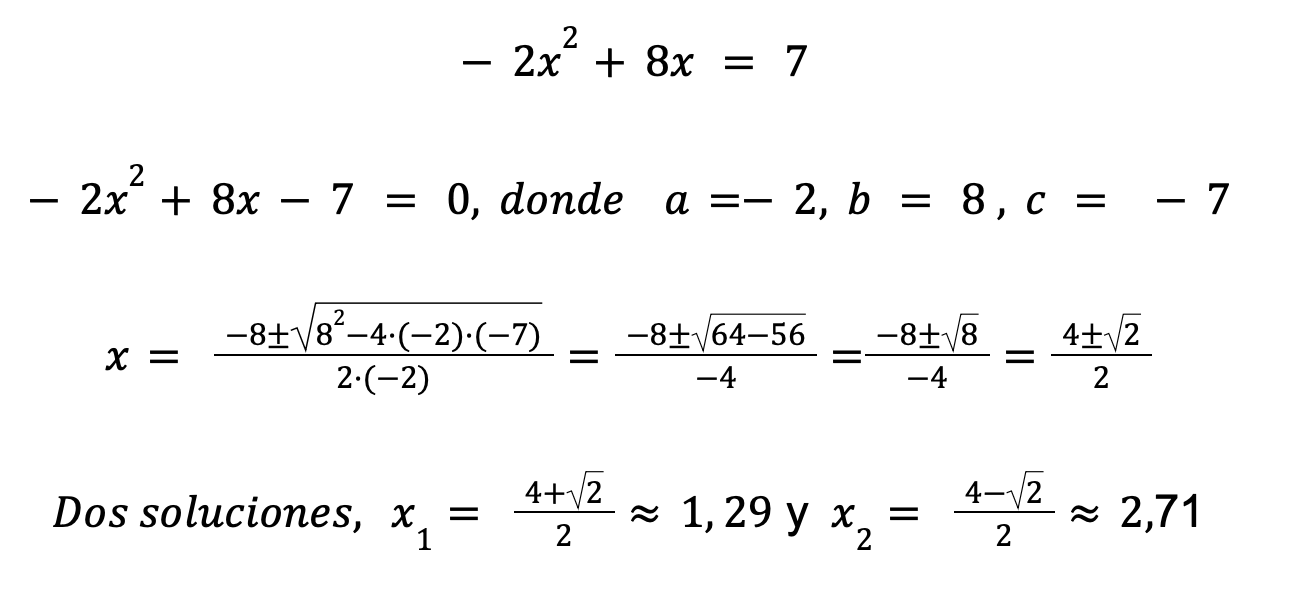
Es decir, cuando la pelota lleva en el aire 1 segundos y 29 centésimas (subiendo) y a los 2 segundos y 71 centésimas (bajando) se encuentra a 7 m. de altura. Lo podéis comprobar en la gráfica de arriba que es así.
Y si os preguntara ahora, ¿en qué momento la pelota alcanza los 10 metros de altura? Me diríais, con toda la razón, si estoy tonto o me pasa algo, porque la altura máxima, ya lo hemos visto, son 8 metros y se consigue a los 2 segundos.
A pesar de mi locura transitoria, insisto en la pregunta, no sea que se nos escape algo. Así que del mismo modo que antes lo vamos a intentar resolver con una ecuación, pero en lugar de que la altura sea 7 metros, igualémoslo a 10 metros.
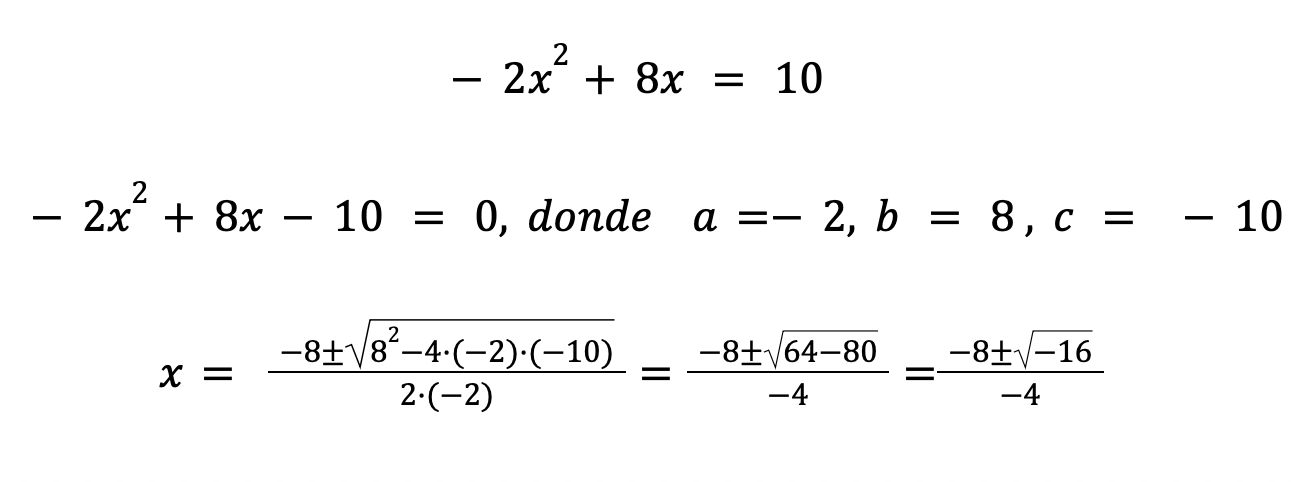
Nos sale una raíz cuadrada de un número negativo y en estos casos les decimos a los alumnos en clase que la ecuación no tiene solución. Todo es coherente con que la altura máxima eran 8 metros y al buscar la solución de la ecuación cuando la pelota llega a 10 metros de altura, no es posible calcularla.
En nuestro mundo “Real”, efectivamente todo concuerda pero y si existiese un mundo “Imaginario” donde fuese posible, ¿qué me decís? Definitivamente, que he perdido totalmente la cabeza, ¿verdad?
Hemos llegado a la cuestión central del artículo de hoy. Definimos raíz cuadrada de un número como:
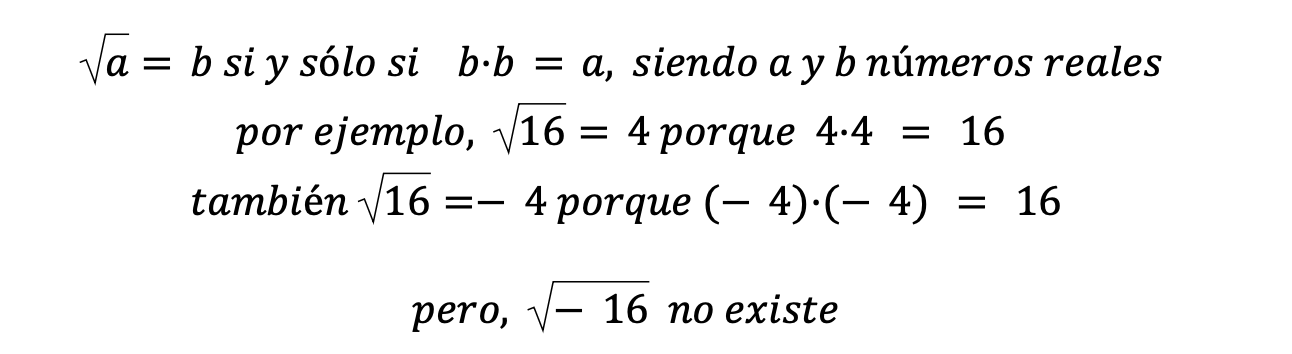
porque no puede haber ningún número que multiplicado por sí mismo dé un número negativo, ni -16, ni ninguno en los números reales.
Hasta el siglo XVI las matemáticas se habían quedado ahí “atascadas”, así que llegó un tal Gerolamo Cardano (1501–1576) y empezó a usar raíces de números negativos al resolver ecuaciones cúbicas en su obra Ars Magna(1545). Y aunque no entendía completamente su significado, admitía su existencia formalmente. Fue Rafael Bombelli (1526–1572) el verdadero pionero en dar sentido a las raíces de números negativos. En su libro Algebra (1572), define cómo operar con raíces negativas y describió las reglas que usamos hoy.
Fijaos la cara que le echaron esta gente, como no existe la raíz de números negativos, se lo inventan. Veamos cómo lo hicieron.
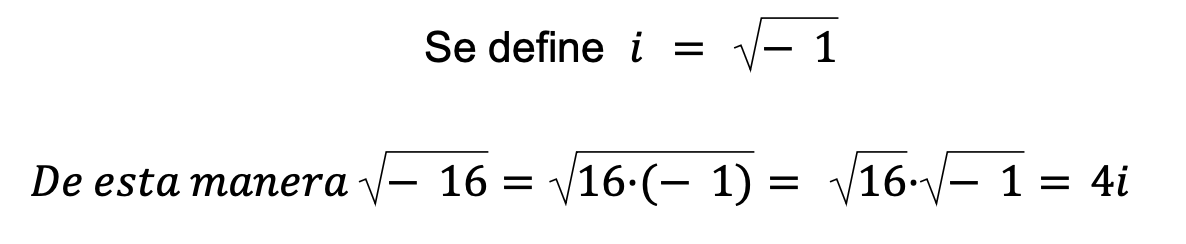
Arreglado el problema y se quedaron tan panchos. Ahora ya, con la ayuda de Cardano y Bombelli, sí tendría sentido resolver la ecuación para que la pelota alcance los 10 metros de altura, retomemos los cálculos:
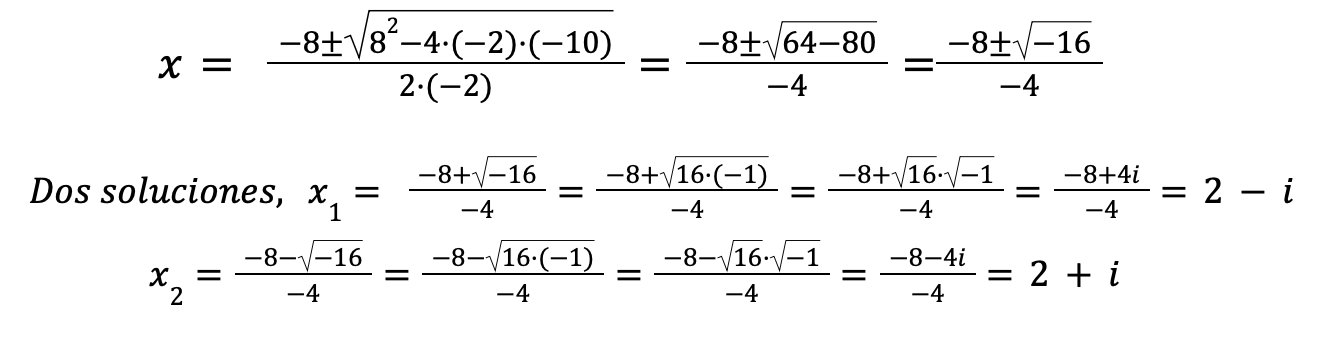
2+i y 2-i, cuántos segundos son esos…Así aparecieron los números complejos, tatachán…
Los números complejos son una forma de extender los números reales para poder resolver ecuaciones que no tienen solución en ellos, como lo que os he planteado anteriormente.
Un número complejo se escribe así:
a + bi
Donde:
-
a es la parte real.
-
b es la parte imaginaria.
-
i es la unidad imaginaria, definida como i2 =−1
Ejemplo:
3 + 2i
-
Parte real: 3
-
Parte imaginaria: 2i
Para representarlos se utilizan los ejes cartesianos y recibe el nombre de plano complejo. En el eje horizontal o eje de abscisas colocaremos la parte real y en el eje vertical o eje de ordenadas la parte imaginaria. La representación de un número en el plano complejo recibe el nombre de afijo.
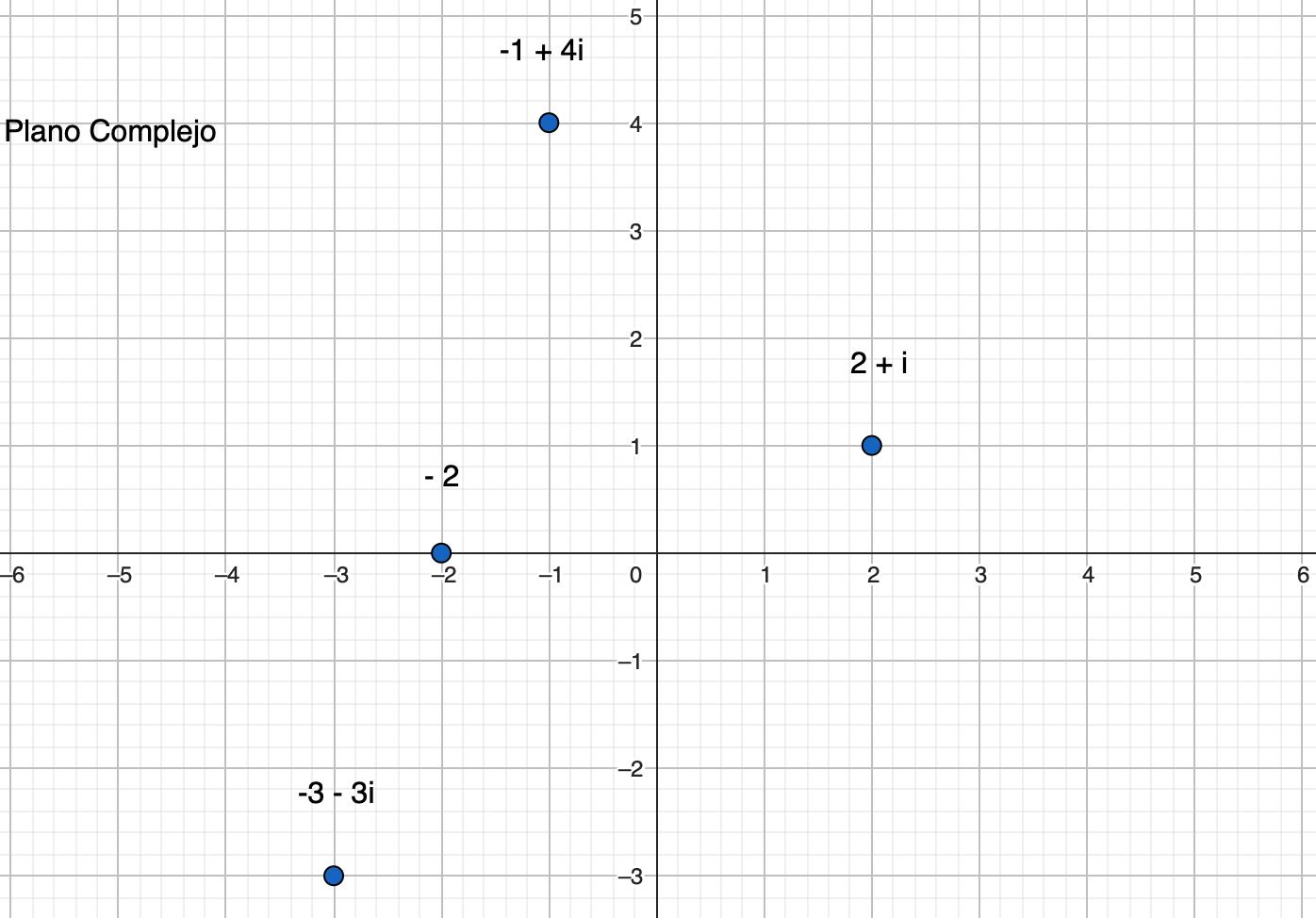
Hasta otra
























