
Te quiero infinito

Estoy seguro que alguna vez os han dicho que os quieren mucho, con todo su corazón, sin medida, ahora y siempre, más de lo que imagináis…. e infinito, os ha dicho que os quieren infinito. Cuidado, porque puede haber truco… No sé si lo sabéis pero hay distintos infinitos y unos más grandes que otros. Y os pregunto, si os quieren infinito, ¿qué infinito es, el natural o el de real?
Supongo que ahora estaréis, además de flipando, elucubrando “qué será mejor, lo natural o lo real en el mundo de los infinitos”
Sí amigos míos, hoy va la cosa de conjuntos finitos e infinitos y de cómo se le fue la perola a Georg Cantor con este tema. Vamos al lío.
Desde la prehistoria, los humanos necesitaban llevar registro de cantidades: cuántos animales cazaban, cuántas personas había en el grupo… Al principio usaban marcas en piedras, huesos o madera (como el famoso hueso de Ishango de hace unos 20.000 años, del que ya os hemos hablado).
Contar es una de las acciones más naturales y primigenias que realizamos. Cuando contamos, lo que hacemos en el fondo es relacionar cada elemento de un conjunto a un número natural. Por ejemplo, si tenemos tres ovejas, las señalamos y decimos: «una, dos, tres». Cada número representa una oveja.
Aquí entra un concepto fundamental en matemáticas: el cardinal de un conjunto. El cardinal es simplemente el número de elementos que tiene un conjunto. Si tenemos el conjunto A = {cuchara, cuchillo y tenedor}, su cardinal es 3, porque hay tres elementos. De manera que cuando los niños aprenden a contar, en realidad están empezando a entender de manera intuitiva, el concepto formal de cardinal en matemáticas.
Vayamos con el primero de nuestros objetivos de hoy, los conjuntos finitos.
Un conjunto finito es aquel en el que podemos contar sus elementos. El número que obtenemos al contar todos los elementos es el cardinal del conjunto, que es un número natural.
Ahora bien, si dos conjuntos finitos tienen el mismo número de elementos podemos establecer entre ellos una relación uno a uno. A cada elemento del primer conjunto le hacemos corresponder exactamente un elemento del segundo conjunto y viceversa.
Pongamos un ejemplo sencillo:
Sea el conjunto A = {manzana, pera, plátano} y conjunto B = {rojo, verde, amarillo}
Podemos hacer la correspondencia:
manzana → rojo
pera → verde
platano → amarillo
Aquí cada elemento de A está emparejado con uno y solo uno de B, y viceversa. Esto es lo que se llama en matemáticas correspondencia biunívoca o biyección. Entonces decimos que A y B tienen el mismo cardinal que es 3.
Hasta aquí todo es muy intuitivo hasta que llega Georg Cantor (1845-1918), matemático alemán considerado el padre de la teoría de conjuntos. Revolucionó las matemáticas al introducir la idea de que no solo se pueden comparar conjuntos finitos, sino también conjuntos infinitos. Estaría aburrido el hombre y se enredó con esto.
Cantor definió los conjuntos finitos A como aquellos en los que no se puede establecer una relación biunívoca con cualquier subconjunto suyo B, distinto de él (propio).
Por ejemplo, si A = {1,2,3,4,5,6,7,8,9,10} y B = {2,4,6,8,10} no es posible construir una biyección entre A y B, porque no tienen la misma cardinalidad (el mismo número de elementos).
Y de esta manera llegamos donde queríamos:
Según Cantor, un conjunto es infinito si es posible encontrar un subconjunto propio del mismo que tenga la misma cardinalidad que el conjunto original. Es decir, que se pueda establecer una correspondencia uno a uno entre ellos.
Consideremos el conjunto de los números naturales N = {0,1,2,3,4,5,…}, veamos si es un conjunto infinito. Para verificar tal afirmación tenemos que encontrar un subconjunto propio y construir una biyección entre ambos. Para este caso, consideremos el subconjunto de números naturales pares P = {2,4,6,8,10,…}. El conjunto P es un subconjunto distinto de N y establecemos la relación:
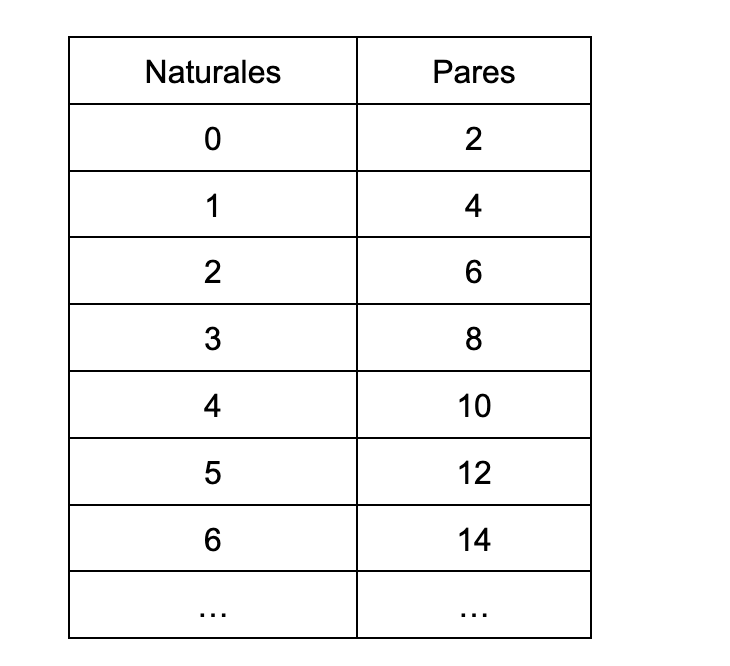
De esta manera a todo número natural le corresponde uno par y viceversa.
Según Cantor, en el mundo de los infinitos, hay la misma cantidad de números naturales que números pares… Ufff, esto empieza a calentarme la cabeza.
Vamos a comparar los números enteros Z = {…-5,-4,-3,-2,-1,0,1,2,3,4,
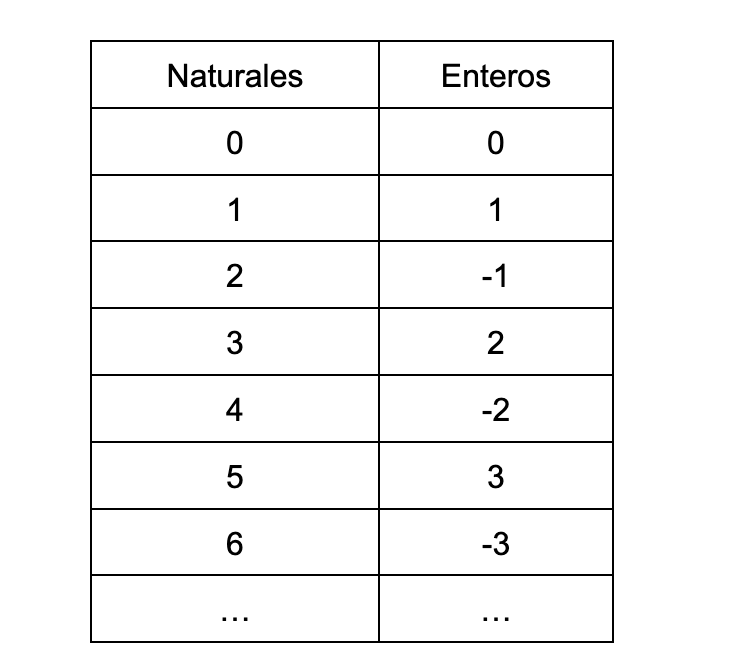
Cantor mediante, los números enteros Z y los números naturales N, que a priori parece que uno tiene el doble de elementos que el otro, poseen el mismo cardinal. Este cardinal recibe el nombre de Aleph-cero, infinito de los números naturales o infinito contable. Cantor, incluso, estableció un procedimiento, el argumento diagonal, para relacionar de forma biunívoca los números racionales Q (fracciones) y los naturales N. Por lo que el cardinal de Q también es Aleph-cero.
Y qué pasa con los números reales R (números decimales). Cantor con su famoso argumento diagonal demostró que, aunque intentes emparejar todos los números decimales entre 0 y 1 con los números naturales, siempre quedará algún número real fuera.
De esta manera probó que los números reales son «más infinitos» que los números naturales. El conjunto de los números reales tiene un cardinal mayor, llamado el cardinal del continuo.
Pero Cantor no se quedó ahí, sino que afirma que no solo hay dos tipos de infinito, sino que en realidad hay infinitos tipos de infinitos, ya que si tienes cualquier conjunto, se puede formar el conjunto de todas sus partes y ese conjunto siempre tiene más elementos que el conjunto original. Una paranoia, vamos.
Volvamos entonces a la pregunta inicial. Si os dicen ahora que os quieren infinito… ¿Pensáis que no se os puede querer más? ¿A vuestra pareja la queréis infinito contable y a vuestros hijos o padres infinito del continuo?…
Yo sólo por estar ahí sí que os quiero infinito, ponerle vosotros el apellido.
























