La reina Dido

Al morir Muto, rey de Tiro, allá por el siglo XIII A.C., la corona pasó a manos de su hijo Pigmalión, el cual tenía una hermana llamada Elisa. Ella estaba casada con Siqueo, sacerdote del templo de Melqart y qué raro, como Pigmalión ansiaba los tesoros de este templo, no se le ocurrió otra cosa que matar a Siqueo (el tridente: violencia, dinero y poder siempre presente a lo largo de la historia). Elisa, no obstante, tuvo tiempo suficiente para, con el apoyo de un grupo de tirios contrarios al rey, escapar con los tesoros de su marido hasta el norte de África.
La zona donde se asentó con su séquito estaba dominada por la tribu de los gétulos, a cuyo rey, Jarbas, le pidió hospitalidad y un terreno para asentarse. Jarbas, para quitársela de encima, le dijo que le daría tanta tierra como abarcara una piel de buey. Elisa, con el propósito de delimitar el máximo territorio posible, cortó la piel en finas tiras para formar una cuerda lo más larga posible y así consiguió circunscribir una amplia extensión de terreno. En él mandó construir una fortaleza llamada Birsa, que tiempo después se convirtió en la ciudad de Cartago. Proclamada como soberana de la ciudadela, recibió de los habitantes el nombre de Dido, la reina Dido.
 Llegaron a estos lugares, donde ahora ves enormes murallas
Llegaron a estos lugares, donde ahora ves enormes murallas
y nace el alcázar de una joven Carthago,
y compraron el suelo, que por esto llamaron Birsa,
cuanto pudieron rodear con una piel de toro. . .
Virgilio, La Eneida.
La leyenda de la fundación de Cartago aparece en el libro IV de La Eneida escrito por Virgilio y de esta forma tan literaria se plantea desde la mitología El Problema Isoperimétrico.
La palabra isoperimétrico significa con el mismo perímetro y lo que buscamos con este clásico problema es encontrar la figura que abarque el mayor área posible teniendo el mismo contorno, el mismo perímetro, la cuerda de piel de buey. Ya os adelanto que Dido dio con esa figura ideal, y vosotros, ¿os aventuráis a apostar por una? Estoy seguro que alguien sí.
Posiblemente el desapego de muchos estudiantes por las matemáticas sea la forma en la que se ha enseñado en muchas ocasiones a lo largo del tiempo, diría que la mayoría de las veces, de manera insustancial, alejado de la realidad, del entorno que nos rodea… Esto podría ser el ejemplo contrario, Dido se encontró con este problema real y debía intentar sacar la mejor de las soluciones porque iba en su beneficio y en el de su pueblo.
Así que nosotros también vamos a intentarlo una semana más. ¿Cómo nos enfrentamos a este problema? Tenemos un perímetro fijo, vamos a suponer que una cuerda de longitud 1000 m., y queremos encontrar la figura que tenga de contorno esa longitud y encierre el máximo área posible.
Para abordarlo propongo que usemos los polígonos regulares: triángulo equilátero, cuadrado, pentágono regular, hexágono regular…
Antes vamos a ponerle nombre a las cosas, lo que en matemáticas se llama notación:
-
P: Perímetro del polígono regular.
-
L: Lado de polígono regular
-
n: Número de lados del polígono regular.
-
A: Área del polígono regular.
-
a: Apotema. Segmento que une el centro de la figura con el punto medio de cualquier lado de un polígono regular.
-
r: Radio. Segmento que une el centro de la figura con cualquier vértice de un polígono regular.
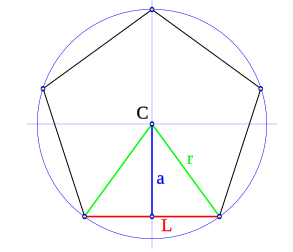
Vamos a probar con el cuadrado y con el hexágono, a ver qué pasa:
Cuadrado
Como el perímetro siempre va a medir 1000 m, P = 1000, cada lado medirá la cuarta parte, L = P/4 = 1000/4 = 250 m.
Como el área del cuadrado es lado x lado, A = L x L = 250 x 250 = 62.500 metros cuadrados.
Hexágono
A partir de un perímetro de 1000 m., en este caso, cada lado medirá la sexta parte, así, L = P/6 = 1000/6 = 166,67 m.
A partir del perímetro de un polígono regular también podemos calcular su apotema, la fórmula es:
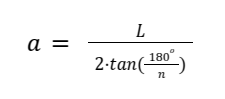
La fórmula es lo de menos, lo que es interesante es que a partir de ella llegamos a que la apotema a = 144,34 m.
El área de un polígono regular es Perímetro x Apotema dividido entre dos:
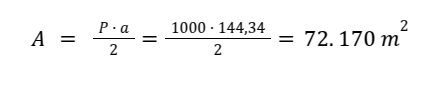
De aquí podemos empezar a intuir la primera hipótesis, en los polígonos regulares con el mismo perímetro, cuantos más lados tenga, encierran mayor área.
Volvamos entonces a la fórmula del área de los polígonos regulares.
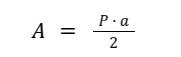
Como el perímetro es el mismo, cuanto mayor sea la apotema, a, mayor será el área, la pregunta que nos hacemos ahora es. En polígonos regulares, ¿cuantos más lados tienen, mayor es su apotema?
Efectivamente, lo podemos afirmar con los polígonos regulares de menor número de lados en la siguiente tabla, todos ellos de 1000 m. de perímetro:
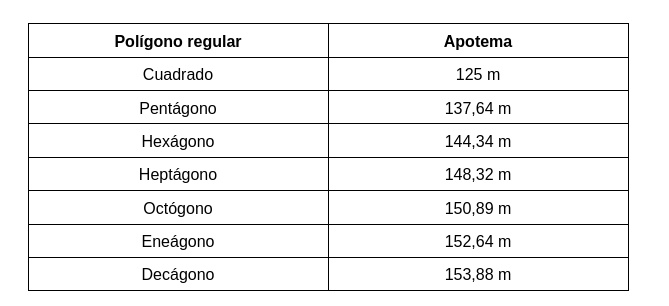
y lo podéis comprobar a través de la fórmula de la apotema que tenéis arriba.
Y a qué figura se parecen cada vez más los polígonos regulares a medida que crece el número de lados….
A la circunferencia, equilicuá, habéis llegado a la misma conclusión que llegó Dido unos siglos después que ella. Ahora solo os falta que os dejen rayar un terrenito para que tengáis vuestro reino.
Pero demostrar que esa figura óptima es la circunferencia le ha dado muchos dolores de cabeza a nuestro “querido” mundo matemático.
El griego Zenódoro (siglo II a.C.) demostró que, entre todos los polígonos regulares con el mismo perímetro, el que tiene más área es el que tiene más lados. También conjeturó que el círculo es la figura óptima, aunque sin una demostración formal. Que es a lo que nos hemos intentado acercar nosotros hoy.
Tuvimos que esperar a que Jacob Steiner en 1838 presentara una demostración usando el método de comparación, sin embargo, su prueba no era completamente rigurosa porque asumió que la solución existía, sin probarlo formalmente.
Pero no fue hasta el siglo XIX cuando Karl Weierstrass introdujo el cálculo variacional, proporcionando las bases para una demostración rigurosa de la existencia de la solución.
Didos y Didas míos, ya andaba la circunferencia, con su Pi, escondido por ahí… Sed buenos.