
El problema del cálculo de área

Desde tiempos muy antiguos, casi podríamos aventurarnos a decir que tras la llegada de la agricultura, el ser humano abandonó paulatinamente el nomadismo y comenzó a cultivar la tierra, surgiendo la necesidad de medir los campos para repartirlos, registrar cosechas y resolver disputas por los límites. En civilizaciones como Egipto, después de las crecidas del Nilo, los agricultores tenían que volver a trazar sus parcelas y calcular cuánto espacio ocupaban. En Mesopotamia también se buscaban métodos para estimar superficies de rectángulos y triángulos en las tablillas de arcilla. Con el tiempo, los griegos dieron mayor precisión a estos cálculos gracias a la geometría, transformando aquellas primeras necesidades prácticas en conocimientos matemáticos más exactos.
Aunque dependiendo de la civilización se usaban distintas unidades de medida, no es nuestro objetivo hoy enredar con ello, por lo que vamos a saltar directamente al sistema métrico decimal y vamos a trabajar con la unidad internacional de medida de longitud que es el metro. Como curiosidad en 1875 se creó el “metro patrón” o “metro de referencia” que era una barra de platino e iridio que se guardaba en la Oficina Internacional de Pesas y Medidas (BIPM) en Sèvres, París, y se utilizaba como estándar para calibrar otros instrumentos de medición. En la actualidad el metro se define en función de la velocidad de la luz como una constante universal y no depende de ningún instrumento físico. ¡No digáis que no os enseño cosas interesantes!
Vamos a lo que nos ocupa hoy que es: ¿cómo medimos una superficie? Ya os digo que el que empezó con esta tarea no andaba muy ocurrente ese día, a mí me da que salió la noche antes. Digo yo, y esto no es ninguna verdad científica, que comenzó con el siguiente cuadrado y dijo:
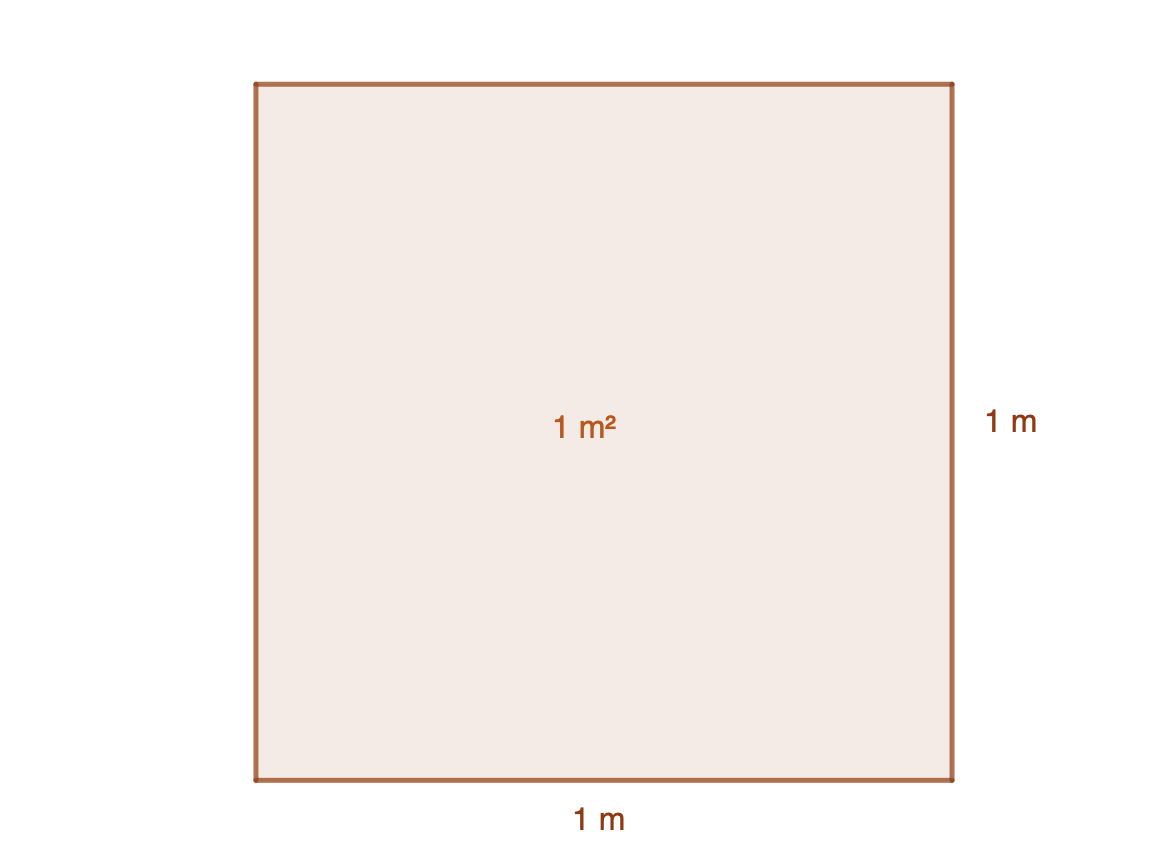
“Los cuadrados de 1 metro de lado, es decir, 1 metro de base y 1 metro de altura van a tener un área o superficie de… 1 metro cuadrado.” Con dos… y se quedó tan ancho.
A partir de ahí podríamos decir que se empieza a construir el cálculo del área del resto de figuras planas. El siguiente paso natural es el cálculo de la superficie de un rectángulo.
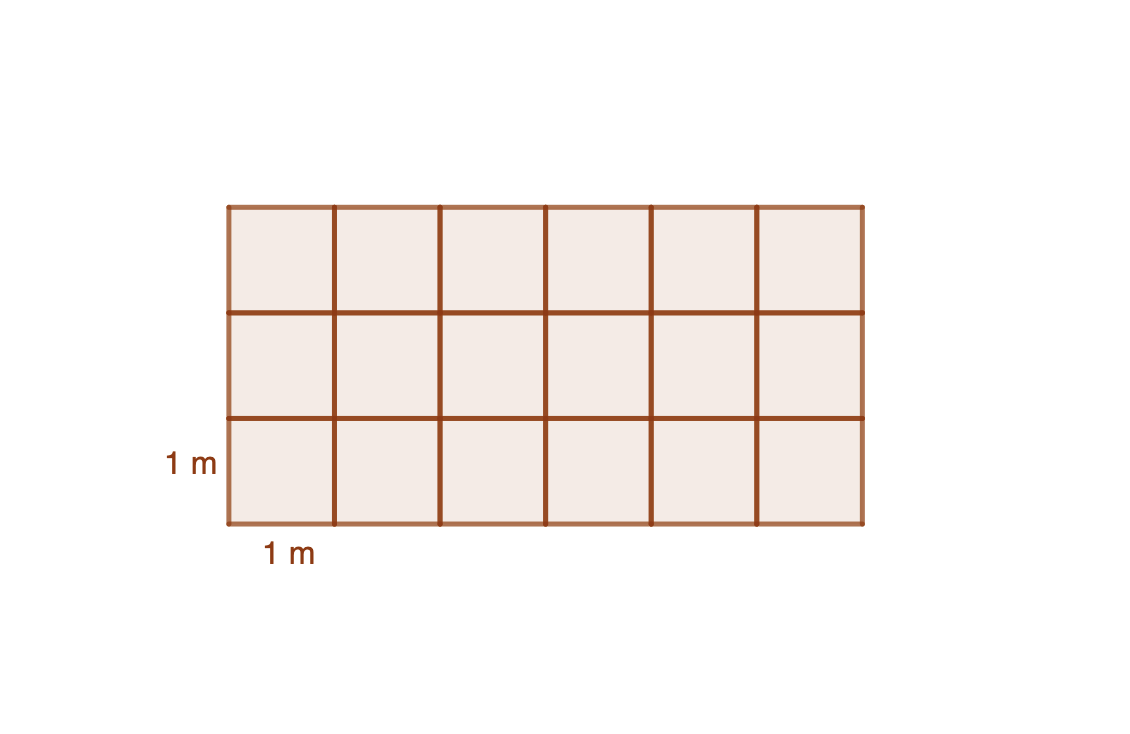
Según lo anterior se trataría de sumar las áreas de los cuadraditos de 1 metro cuadrado en los que se divide el rectángulo. Éste concretamente está formado por 18, por lo que su área podríamos decir que es de 18 metros cuadrados.
Pero si nos damos cuenta y multiplicamos el número de cuadrados en horizontal, la base, por el número de cuadrados en vertical, la altura, en este caso 6 x 3, nos da los 18 metros cuadrados. Por lo que de aquí podemos deducir de dónde podría salir la fórmula del área del rectángulo.

Pero es que a partir de aquí ya no es necesario saber nada más sobre áreas, porque aunque no lo creáis, el resto de figuras planas las podemos reducir al cálculo del áreas de rectángulos, bueno y triángulos, pero es que un triángulo es medio rectángulo. ¿Lo vemos?
Si el triángulo es rectángulo es muy claro.
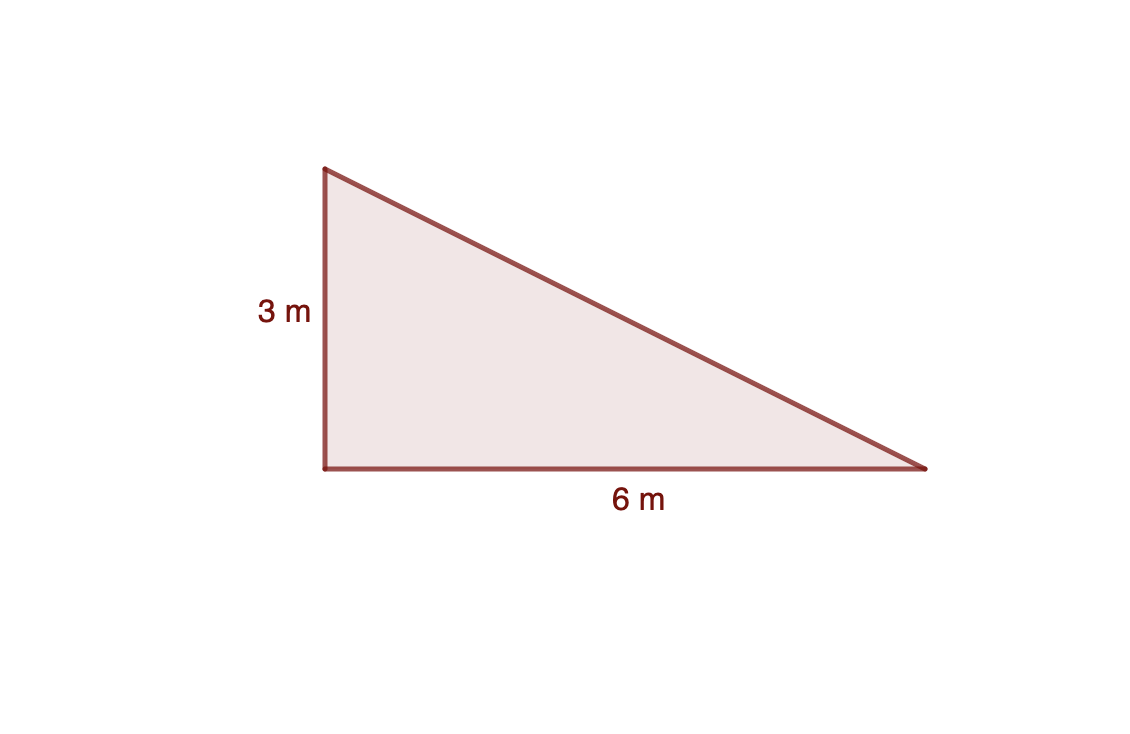
Se comprueba fácilmente que es la mitad de un rectángulo.
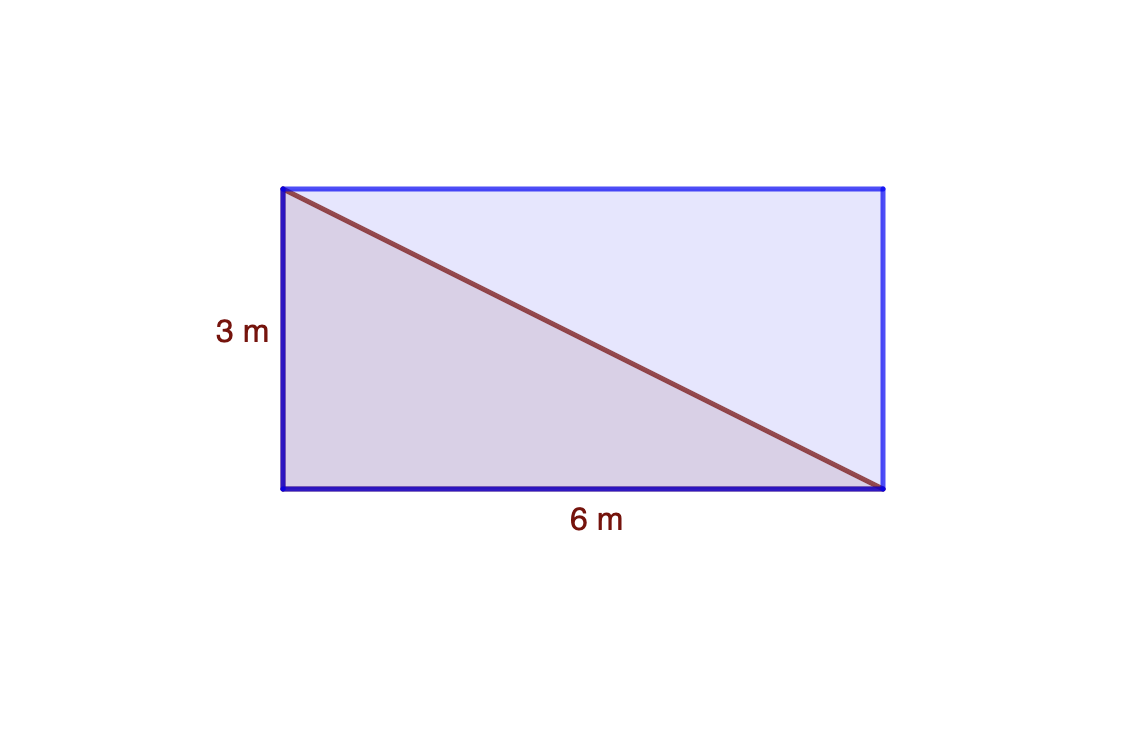
Pero qué pasa con el resto de triángulos. Que también lo cumple, lo vamos a demostrar con un triángulo acutángulo, para triángulos obtusángulos simplemente tendríamos que girarlos y colocar de base el lado opuesto al ángulo obtuso (mayor de 90º).
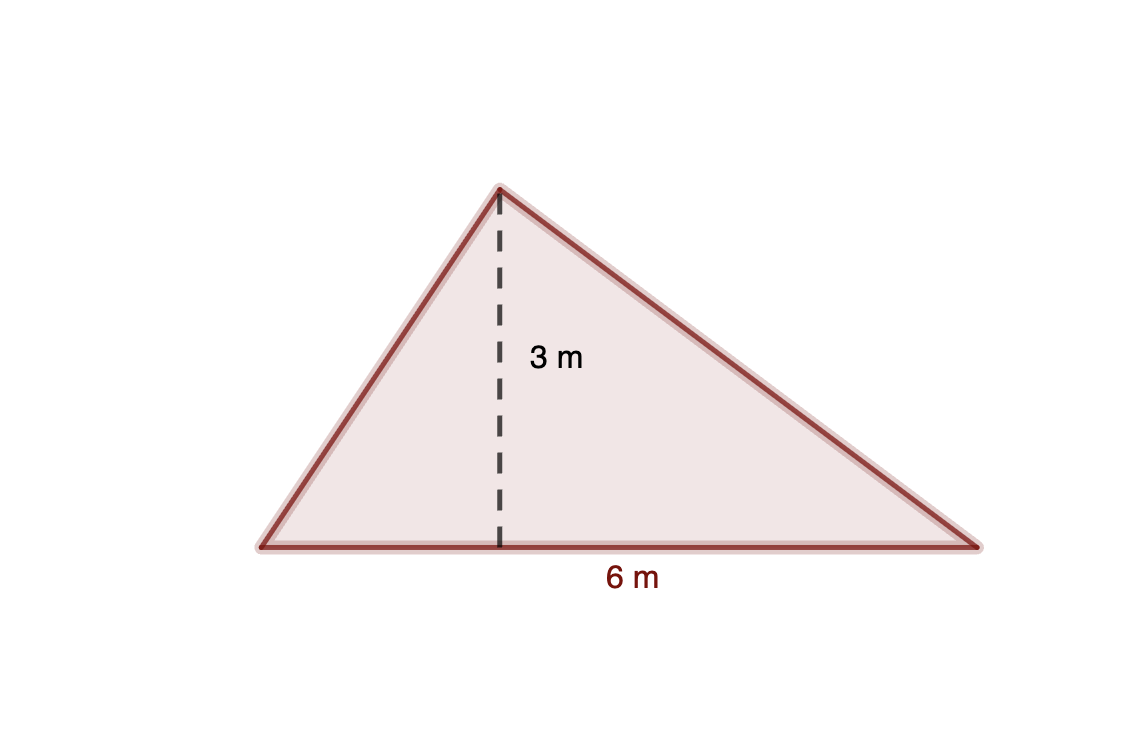
Dividimos el triángulo dado en dos triángulos rectángulos, como cada uno ya sabemos que es la mitad de un rectángulo, la unión de los dos es otro rectángulo que precisamente ocupa el doble de superficie que el triángulo inicial. Podéis comprobarlo en esta descomposición.
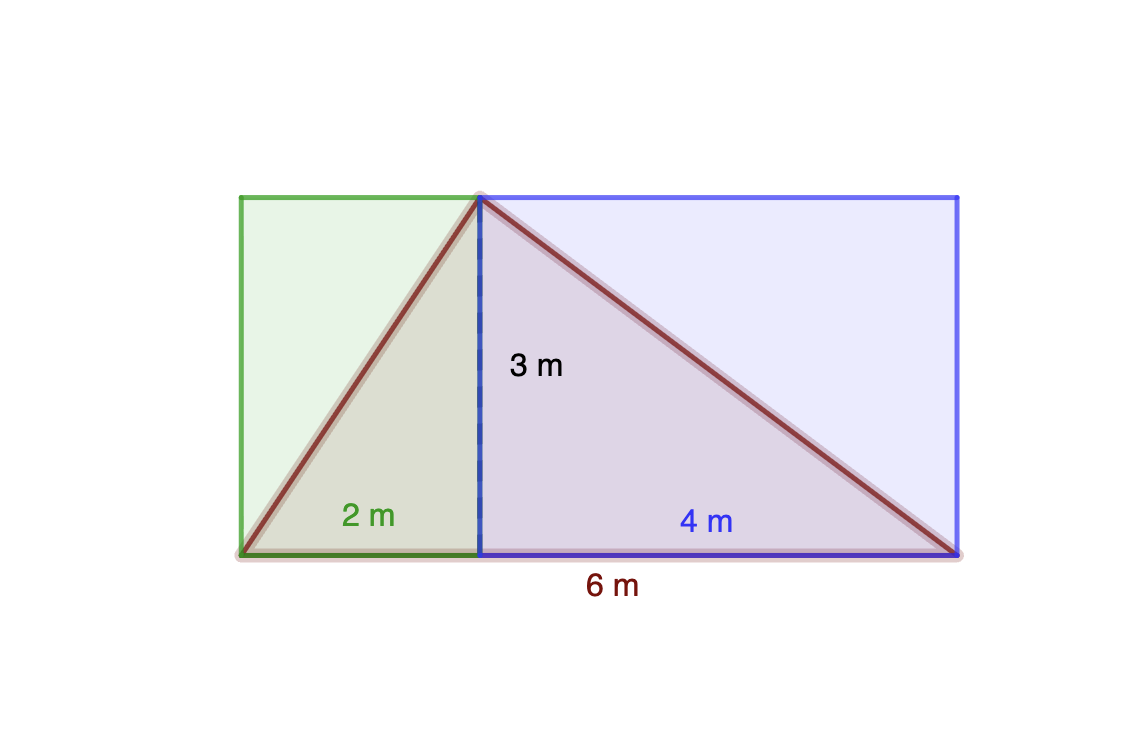
De ahí podemos deducir que el área de un triángulo es la mitad del rectángulo con su misma base y altura.

Y hemos terminado, porque cualquier otro polígono lo podemos descomponer en la unión de triángulos, así que calcular el área de cualquier polígono se reduce a saber calcular el área de estos triángulos, que a su vez son medios rectángulos.
Os dejo un polígono cóncavo, para que veáis que se cumple con cualquiera que elijamos.
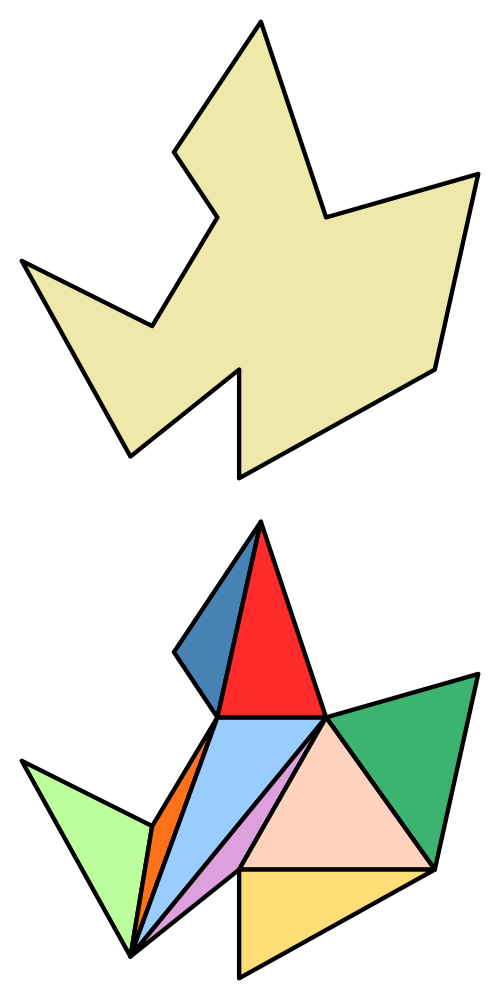
Esto que acabamos de mostrar es el método de cálculo de áreas que se utiliza en topografía y que recibe el nombre de “triangulación de un polígono” o “área poligonal”. Consiste en la división del área en un conjunto de triángulos que cumplen las siguientes condiciones: La unión de todos los triángulos es igual al polígono original y los vértices de los triángulos son vértices del polígono original. Esto es en realidad lo que hacen las máquinas para calcular áreas.
Así que después de llevar toda la vida aprendiendo fórmulas de áreas de figuras con la “base x altura” nos valía… Ya os digo que los matemáticos nos lían, y mucho, algunas veces.
Pero sé que algunos de vosotros ya estaréis pensando, “muy bien hater, pero qué pasa con las figuras limitadas por líneas curvas, no me digas que eso lo arreglas también con los rectángulos”. Pues sí, también se calcula gracias a ellos.
Descomponiendo y realizando los giros necesarios siempre lo vamos a poder descomponer en superficies debajo de trozos de esa curva, seguro que a alguno de vosotros esto ya os empieza a sonar.
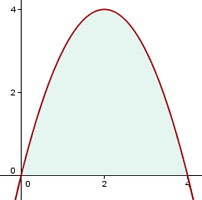
¿Y cómo lo hacemos? Os lo cuento en este vídeo y tenéis que verlo porque sino no se entiende lo que viene detrás.
https://www.youtube.com/watch?
Si denotamos

Y curiosamente ese área en matemáticas es lo que conocemos como integral definida. Tatachannnnnn
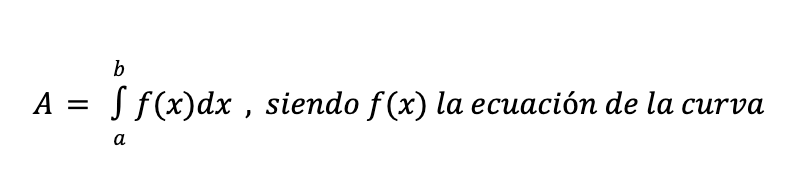
Sin tener ni idea hemos llegado al concepto de integral definida simplemente conociendo cómo se calcula el área de de un rectángulo.
¿Para qué tantas fórmulas de áreas de figuras?






















