El número de oro (II)

Como el título indica, este artículo es la segunda parte del que titulamos El número de oro (I) en la sección de El hater matemático, el cual recomiendo leer para seguir el hilo, si no lo habéis hecho aún. 

Para ponernos en situación, el número de oro lo llamábamos con las letras griegas φ (phi) (en minúscula) o Φ (Phi) (en mayúscula), era un número racional y algebraico, tenía un valor aproximado a 2,618 y os recuerdo que fue Euclides el primero en definirlo y lo hizo del siguiente modo: 

Dado un segmento de longitud a + b, diremos que está dividido en media y extrema razón, también conocida como sección áurea o proporción áurea si cumple que la longitud total del segmento dividido entre su parte mayor es igual a esta última entre la parte de menor longitud. 

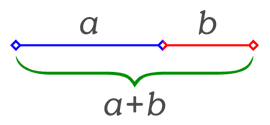
Es decir 

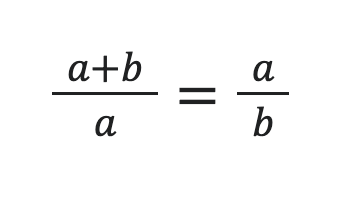
Y a que no os imagináis qué valor toman estos dos cocientes independientemente de la longitud del segmento que tomemos. Efectivamente, φ, el número de oro. Primera casualidad del día.  

Vamos a verlo:

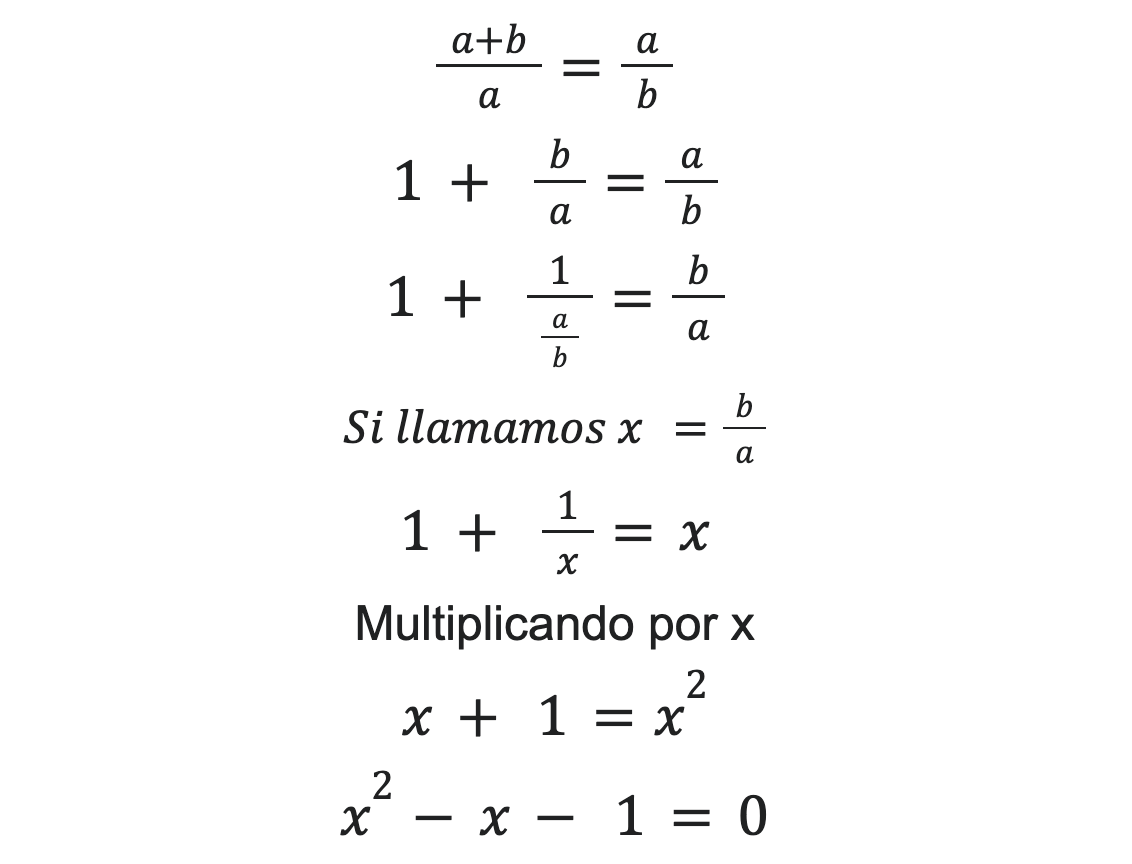
Si recordáis, la solución positiva de esta la ecuación, como vimos en el artículo anterior, es:

El mismo Euclides fue quien realizó la construcción geométrica del número de oro con regla y compás. 

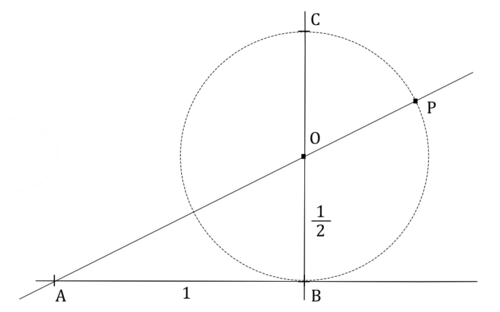
Trazando dos segmentos AB y BC perpendiculares e iguales de longitud 1. Con centro en O se traza la circunferencia de radio 1/2. Finalmente, uniendo A con O y prolongando hasta la circunferencia obtenemos P. La longitud AP es el número áureo.

Esta misma construcción es válida para crear segmentos áureos independiente de la longitud a AB y BC, siempre que sean de igual longitud y perpendiculares entre sí. El segmento AP con una división interior de longitud AB siempre será una sección áurea. 

Supongo que a estas alturas os habréis preguntado por qué el apelativo de áureo (parecido al oro o dorado). La primera vez que se tiene constancia de la aparición de este adjetivo para referirse al número que nos ocupa lo hace el matemático alemán Martin Ohm, en la segunda edición de su libro Die Reine Elementar Matematik (Las matemáticas puras elementales) en 1835. 

Ohm escribió en una nota al pie:

“Uno también acostumbra llamar a esta división de una línea arbitraria en dos partes como estas la sección dorada.”

De forma análoga, decimos que un rectángulo es áureo si la razón entre el lado largo y el corto es exactamente el número de oro. 

También fue Euclides el primero en construir el rectángulo áureo. La construcción la hizo con regla y compás en la proposición 2.11 de Los Elementos y resulta que coincide 24 siglos después con las dimensiones de las tarjetas de crédito, el DNI o el carnet de conducir, sí señoras y señores, estos documentos son rectángulos áureos. ¿Cómo os quedáis?

Una vez definidos los segmentos y los rectángulos áureos, ¿alguno de vosotros hicisteis la prueba de dibujar un segmento y dividirlo en dos partes de distinta longitud y/o pintar el rectángulo del artículo anterior? ¿Os salieron cálculos cercanos a 1,6? Si es así, inconscientemente os estabais acercando a la sección áurea. A lo que desde la antigüedad se conoce como ideal de belleza y armonía. Por qué, lo veremos un poquito más tarde, porque todavía no he acabado con la geometría y su relación con este número.

Si dibujamos un pentágono regular y trazamos sus diagonales uniendo con segmentos dos vértices como se indica en la siguiente figura: 

Se forma una estrella que recibe el nombre de pentagrama. Resulta que si realizamos algunas mediciones sale lo siguiente:

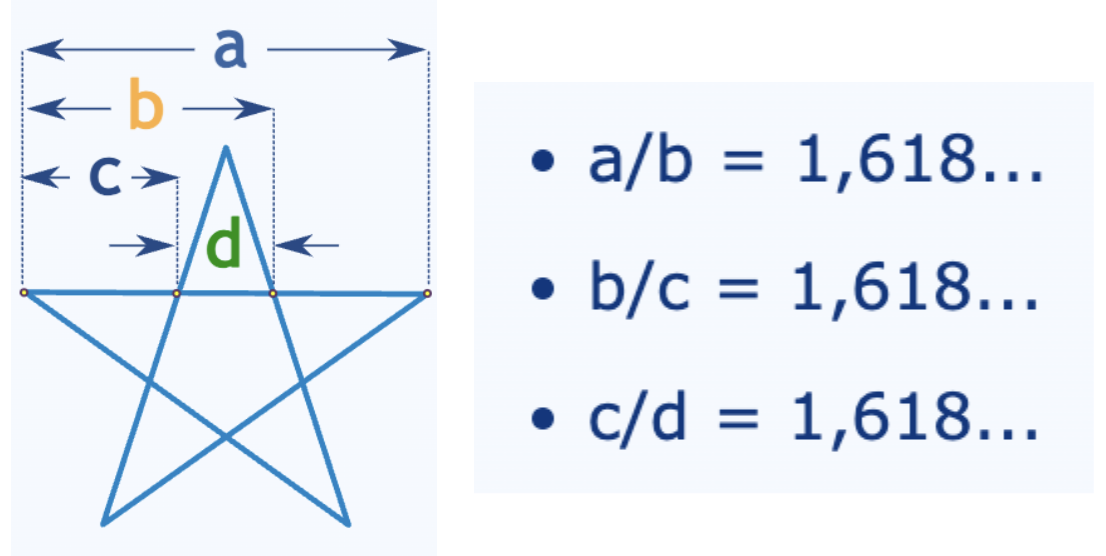
Uyuyuy… que φ anda por aquí cerca de nuevo, otra casualidad. 

Además dijimos en el artículo anterior que el número de oro admitía una expresión trigonométrica:

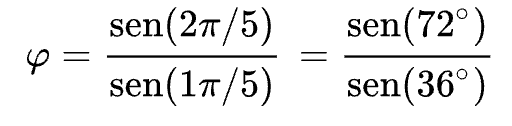
Y es que resulta que 72º es exactamente el ángulo central del pentágono y 36º la mitad. No me digáis que se están alineando los planetas.   

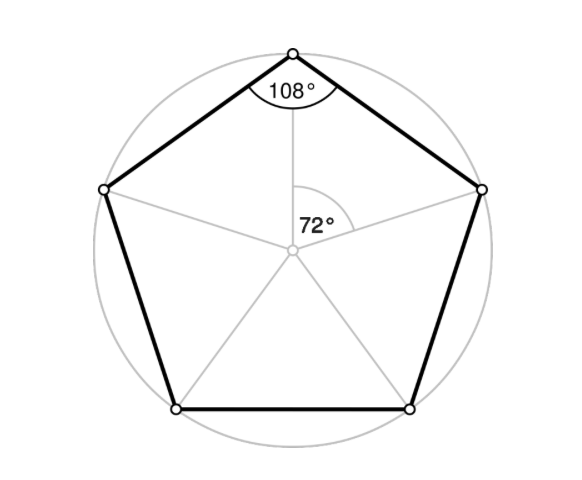
Para terminar con la geometría os dejaré una muestra, que no la única, de la relación del número de oro con los sólidos platónicos (poliedros regulares y convexos, cuyas caras son todas iguales y regulares).

En un dodecaedro (sus caras son 12 pentágonos regulares) con aristas de longitud a, su volumen y su área total se pueden expresar también en términos del número áureo:

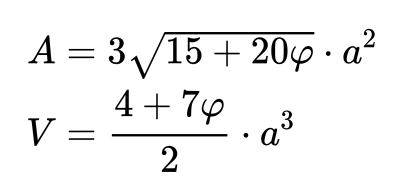
Lo que está dando de sí el numerito, dejaremos las aplicaciones para un tercer artículo, pero no os dejéis impresionar, todo es fruto del azar. El mundo es puro azar.