Menos por menos es más

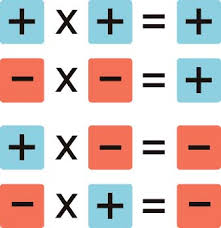
Este título posiblemente sea una de las frases que más quebraderos de cabeza me ha dado como profesor mates y por el que he pasado de puntillas en más de una ocasión cuando me ha tocado explicarlo. La pregunta por parte de los alumnos llega inexorablemente a poco que haya alguna mente medianamente inquieta en el aula: “pero Chepe no entiendo eso de menos por menos es más…”.

Mis salidas han ido desde “eso es para que los números enteros cumplan unas propiedades como estructura numérica. Algo que se da a niveles superiores, cuando vayáis a la universidad y estudiéis matemáticas más profundas”, a lo que que no falta nunca el comentario “pueden esperar tranquilos los de la universidad a que yo estudie matemáticas…jajaja” o algo por el estilo. Otras veces he contestado “esto es así, ya veréis que de esta manera todo funciona…”  pero al mirar la cara del chico o chica que lo ha preguntado se puede comprobar de un golpe de vista que su duda no ha quedado resuelta y como docente, el no saber o poder resolver una duda a un alumno es uno de los momento más incómodos de nuestra profesión… En cualquier momento nos puede pasar, porque los niños o jóvenes son impredecibles, pueden salir por donde menos esperamos y pillarnos en un renuncio, a eso estamos acostumbrados y tenemos tablas para saltar el charco, pero este del “menos por menos, más” ya sabemos que nos va a llegar y os puedo asegurar que no es nada sencillo solucionarlo con un lenguaje acorde a su edad, el objetivo de hoy es intentar hacerlo.

Para ello es necesario entrar en el mundo de los números enteros que nacen de una necesidad humana, como el resto de estructuras numéricas a las que muuuuuchos años después se les dota de empaque matemático. 

Mientras que la caza y la recolección requerían poco más que contar (números naturales), el comercio obligó a la mente humana a dar un salto hacia la abstracción de lo «negativo». El “tener” y el “deber” requerían de una ampliación de lo hasta ese momento era conocido que se instauró de modo natural al día a día.

El conjunto de los números enteros, denotado por el símbolo Z (del alemán Zahlen, «números»), es una estructura numérica que amplía a los números naturales para permitir la expresión de cantidades negativas y la resolución de restas donde el minuendo es menor que el sustraendo.

Se compone de tres elementos fundamentales:

• Enteros positivos (Z+): Coinciden con los números naturales (1, 2, 3…) y representan cantidades acumuladas, alturas sobre el nivel del mar o dinero líquido… 

• El cero (0): No es positivo ni negativo. Actúa como elemento neutro y es el punto de referencia o equilibrio absoluto.

• Enteros Negativos (Z-): Son los opuestos de los números naturales (-1, -2, -3…). Representan deudas, profundidades, temperaturas bajo cero, retrocesos…

Además es necesario dotarlos de un órden: 

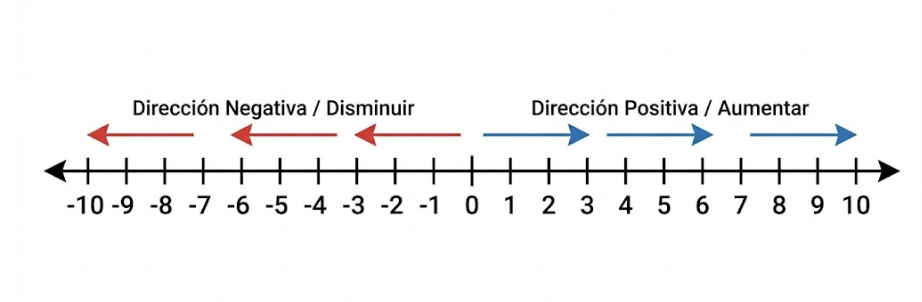Dados dos números enteros a y b:

• a < b (a es menor que b) si a está a la izquierda de b en la recta numérica horizontal. 

Propiedades fundamentales:

1. Cualquier número positivo es mayor que cualquier negativo.  

2. El cero es mayor que cualquier negativo y menor que cualquier positivo.

3. Dados dos números negativos, es mayor el que se encuentra más a la derecha en la recta numérica horizontal. 

La representación se puede realizar de forma análoga en una recta númerica vertical colocando los positivos por encima del cero y los negativos por debajo identificando el orden de menor a mayor con la dirección de abajo hacia arriba. 

Pero, ¿podemos datarlos históricamente? Existen tres hitos, no concretamente definidos pero sí aproximados en en el tiempo que podrían valernos:  

1. La China antigua y las varas de colores

En la China de hace más de 2000 años (Dinastía Han), no usaban el signo «menos» (−), sino un sistema físico de varillas de bambú o madera sobre un tablero.

Como curiosidad usaban las varillas rojas para representar cantidades positivas (al revés que nosotros) y las negras para cantidades negativas. No los veían como «números» en sí, sino como procesos de sumar y restar. Si un comerciante tenía varas rojas, eran ganancias; si eran negras, deudas.

Para los chinos de aquella época, estar en “numeros rojos” era que manejaban guita.

2. La India y el padre de los negativos» (Brahmagupta).

En el siglo VII, el matemático indio Brahmagupta dio el paso de gigante: trató al cero y a los negativos como números con nombre propio.

A los números positivos los llamó «fortunas» (dhana) y a los negativos «deudas» (rina). Un dato relevante es que Brahmagupta escribió reglas que hoy seguimos usando:

• «Una deuda restada a la nada, se convierte en una fortuna» (0 − (−2) = 2).

• «La suma de dos deudas es una deuda aún mayor» (−2) + (−3) = −5.

• «El producto de dos deudas es una fortuna» (Menos por menos es más). 

Cuidadín que Brahmagupta ya lo decía, este recurso no se me ha ocurrido usarlo nunca como explicación para los chicos,  “porque así lo dijo Brahmagupta, y listo”.

Gracias a él, el cero dejó de ser un hueco vacío para ser un número que separa las fortunas de las deudas.

3. Europa y los «números absurdos»

Aunque en Oriente ya se usaban, a los matemáticos europeos les costó siglos aceptarlos. Los llamaban numeri absurdi (números absurdos) o ficti (ficticios).

Para los matemáticos de la época, un número debía representar algo que se pudiera tocar o medir (3 manzanas, 5 metros). ¿Cómo se podía entender «menos 3 manzanas»? No tenía sentido físico.

• Diofanto de Alejandría: Al resolver ecuaciones, si le salía un resultado negativo, decía que la ecuación no tenía solución. Os suena algo relacionado con las de segundo grado, ¿verdad?

• Michael Stifel (s. XVI): Un monje alemán que los llamó «números absurdos» porque estaban por debajo de la nada (el cero).

No fue hasta el siglo XVIII, con matemáticos como Euler, cuando se entendió que los negativos eran fundamentales para el álgebra y para representar direcciones (como en los mapas o termómetros).

A partir de ahora vamos a introducir dos conceptos nuevos íntimamente relacionados con los números enteros: el valor absoluto y el opuesto.

Se define la valor absoluto de un número entero a, y lo representaremos por |a|, a la distancia (positiva) de a al 0. 

Se define el opuesto de un número entero a, y lo denotaremos como Op(a), como  otro número entero que tiene el mismo valor absoluto que a y signo distinto, es decir, si a es positivo, Op(a) será negativo y si a es negativo, Op(a) positivo.

Normalmente nos encontraremos por ahí que Op(a) = – a.

Veamos unos ejemplos sobre valor absoluto y el opuesto de varios números enteros. 

Op(-5) = +5 , Op(3) = -3, |-5| = 5,  |+9| = 9

Comúnmente solemos decir que para calcular el valor absoluto, le quitamos el signo o lo dejamos positivo y al opuesto se le cambia el signo. 

Con estos mimbres ya podemos empezar a elaborar nuestros cestos. 

Comencemos con la suma:

Se trata de conservar el sentido que la operación tenía en los números naturales (los positivos) y ampliarlo a los negativos. 

Así que vamos a entender las cantidades positivas como tenencia, posesión y las negativas como una deuda. 

Veamos los casos que nos podemos encontrar: 

Suma de dos números positivos:

(+3) + (+7)  = +10 → Tengo 3 € y me dan otros 7 €, al final nos quedan 10 €.

Suma de un número positivo y uno negativo:

(-3) + (+7)  = + 4 → Debo 3 € y me dan 7 €, pago los 3 € que debo y aún me quedan otros 4 €.

(+8) + (-9)  = -1 → Tengo 8 €, compro algo con valor de 9 €, pago con los 8 € que tengo y la dependienta me dice que le debo 1 eurillo. 

Suma de dos números negativos:

(-4) + (-9)  = -13 . Debo 4 €, compro algo con valor de 9 €, me he quedado la cartera en casa y la dueña me dice que no me preocupe, que ya le pagaré los 13 € que le debo. 

Para sumar números enteros se suele prescindir de los paréntesis y las operaciones anteriores nos las podemos encontrar como: 

(+3) + (+7)  = + 3 + 7 = + 10

(-3) + (+7)  = – 3 + 7 = +4 

(+8) + (-9)  = + 8 – 9 = -1 

(-4) + (-9) = – 4 – 9 = -13

Sigamos con al resta: 

La resta de dos números enteros se define como el primero más el opuesto del segundo, de esta manera también conserva el sentido que esta operación tiene en los naturales y se amplía a los enteros: 

(+3) – (+7) =  (+3) + Op(+7) = (+3) + (-7) = + 3 – 7 = – 4

 (-4) – (-9) = (-4) + Op(-9) = (- 4) + (+9) = -4 + 9 = + 5  

Pero vamos a los que nos interesa en el día de hoy, el producto o multiplicación: 

Suponed un director de cine que quiera mostrar una escena de una persona caminando por el campo. La secuencia se va a grabar en el croma y luego se le pone el fondo se desee.

El director le dice a la actriz que le va a grabar tres pasos simplemente y que luego repite la secuencia las veces que haga falta. 

En primer lugar le indica que dé tres pasos hacia adelante. Si tuvieseis que transcribir esos tres pasos como un número entero entiendo que escribiriais +3.

Luego le dice que dé tres pasos hacia atrás y la graba ¿Qué número le podríais? – 3, ¿verdad? Seguidamente la manda al camerino porque su trabajo ha terminado y el director se mete en la sala de montaje. 

Tenemos dos números enteros +3 y -3, uno positivo y otro negativo. Ahora vamos a repetir la secuencia siete veces y ya tenemos a nuestra paseante por el campo con un fondo apropiado. 

Pero el director, esas repeticiones, las va a realizar hacia adelante (play) (+7) y hacia atrás (reverse) (-7).

Ahora os pregunto a vosotros, queridos lectores, que pasa si repetimos la secuencia de los tres pasos hacia adelante siete veces en sentido (play)…. Efectivamente la chica da 21 pasos hacia adelante. 

(+7) · (+3) = + 21

Y si repetimos la secuencia de los tres pasos hacia atrás siete veces en sentido (play), queeeee la chica da 21 pasos hacia atrás. 

 (+7) · (-3) = – 21

Ahora vamos a repetir la secuencia de los tres pasos hacia adelante, siete veces hacia atrás (reverse). Vamos a ver como la chica da 21 pasos hacia atrás.

 (-7) · (+3) = – 21

Y llegamos al momento cumbre de este artículo. 

Qué vamos a ver si reproducimos la secuencia de los tres pasos hacia atrás siete veces en sentido (reverse). Sí señores y señoras, 21 pasos hacia adelante. Si tienen cierto manejo con los editores de vídeos, pruébenlo. 

(-7) · (-3)= + 21

Y hasta aquí puedo leer, no sé si hoy lo hemos conseguido u os habéis quedado con la cara como mis alumnos. 

Ya me contaréis.