
Las cónicas
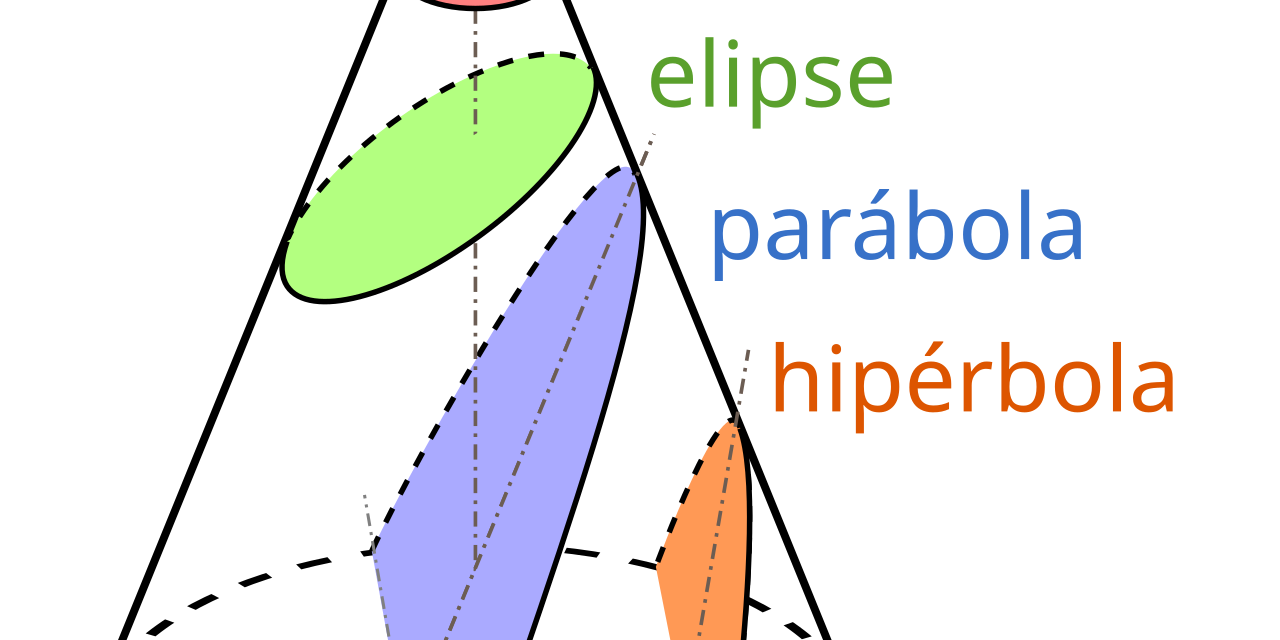
Queridos amigos veréis la que han liado estos matemáticos con dos rectas y un plano. Esto es estirar el chicle de lo lindo.
Esta historia comenzó, como hemos dicho, con dos rectas en el espacio, tomaron una vertical, que la llamaron Eje (e) y otra oblicua que la cortaba en un punto llamado Vértice (V). Esta segunda recibió el nombre de Generatriz (g). Así la cosa quedaba muy sosa por lo que decidieron darle movimiento, “giremos la Generatriz (g) 360º en torno al Eje (e) a ver qué pasa” y así se formó una figura que seguro os suena, ¿verdad?
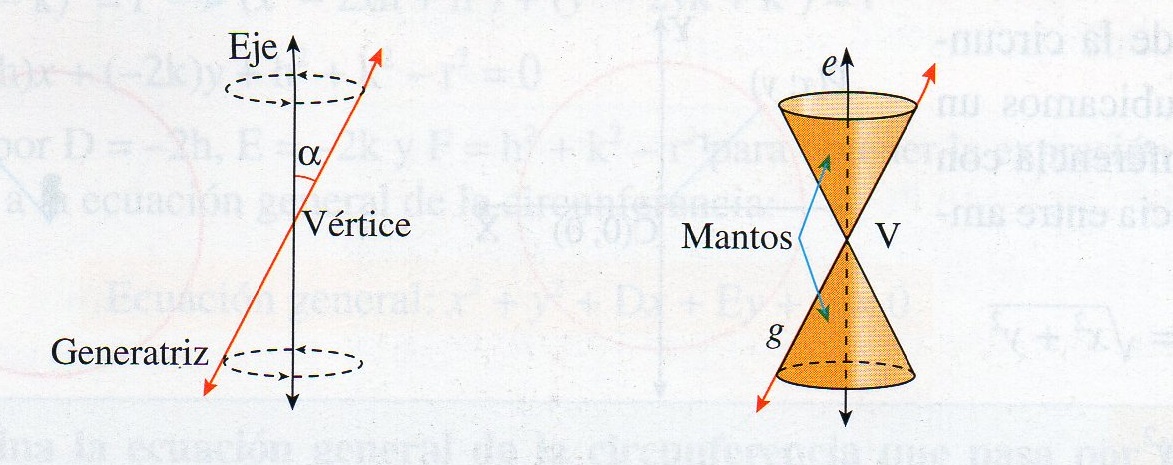
Efectivamente, es un cono, para ser más precisos, un doble cono y cada uno de ellos recibe el nombre de Manto en esta figura, que se han formado por rotación de la generatriz en torno al eje.
En nuestro día a día, los conos aparecen de forma constante tanto en entornos urbanos como en la naturaleza y el hogar. Al caminar por la ciudad, es habitual ver conos de tráfico de color naranja flúor que delimitan zonas de obras o accidentes, mientras que en los supermercados las zanahorias y otros vegetales exhiben esta forma geométrica natural. En el ámbito gastronómico, el cono de helado es el ejemplo más icónico, diseñado para ser una herramienta comestible y ergonómica. Incluso dentro de nuestro propio cuerpo, dependemos de los conos de la retina para distinguir los colores del entorno, y al mirar hacia los parques, las piñas de los pinos (coníferas) nos recuerdan que esta estructura es fundamental para la reproducción de muchas especies vegetales.
Pero se vé que no quedaron tranquilos con esta construcción, que añadieron otro ingrediente más al menú, un plano y se preguntaron, “vamos a ver qué pasa si hacemos la intersección de un doble cono con un plano en el espacio”.
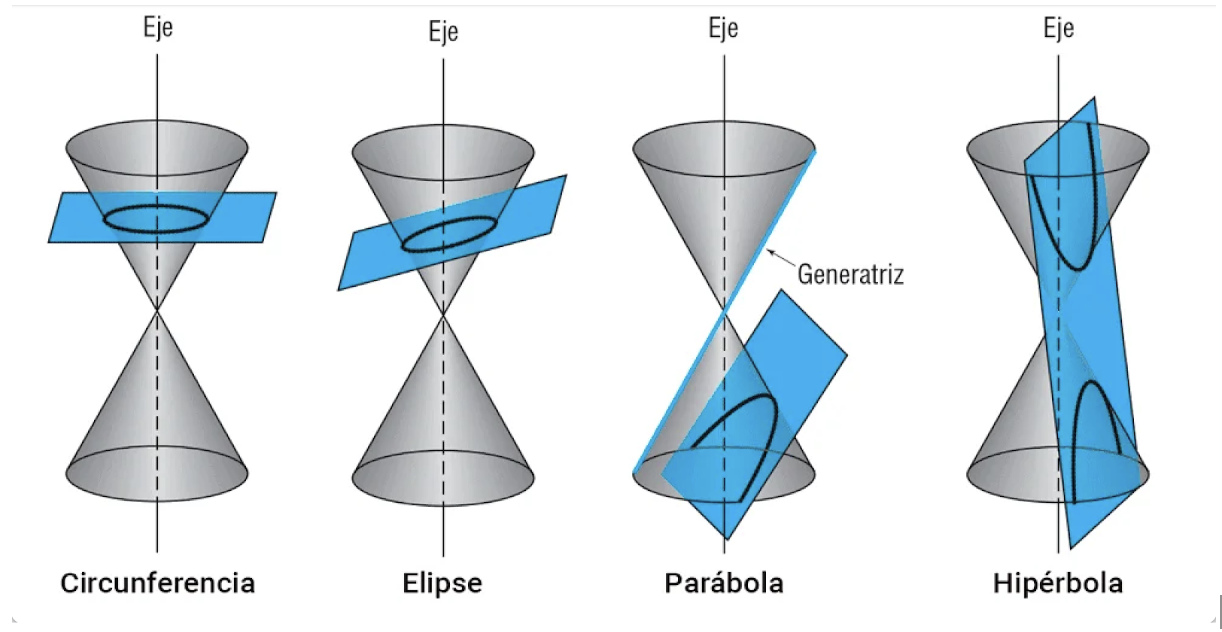 Ahí lo tenéis, dependiendo de la forma en que coloquemos el plano, nos da una figura u otra. Esa “forma de colocar el plano” no es más que la inclinación que le demos a la hora de cortar el cono.
Ahí lo tenéis, dependiendo de la forma en que coloquemos el plano, nos da una figura u otra. Esa “forma de colocar el plano” no es más que la inclinación que le demos a la hora de cortar el cono.
En matemática, y concretamente en geometría, se denomina sección cónica (o simplemente cónica) a todas las curvas resultantes de las diferentes intersecciones entre un cono recto y un plano.
Dependiendo de la inclinación que le demos al plano se obtienen estas curvas planas denominadas circunferencia, elipse, parábola e hipérbola.
Para hallar las distintas secciones cónicas en un cono circular recto, se analiza la relación entre dos ángulos fundamentales: a (el ángulo que forma la generatriz con el eje del cono) y b (el ángulo que forma el plano de corte con ese mismo eje).
Dependiendo de esta relación, se obtienen las siguientes figuras:
-
Circunferencia: Se produce cuando el plano de corte es perpendicular al eje del cono. En este caso, el ángulo b = 90º.
-
Elipse: Se obtiene cuando el plano corta una sola hoja del cono (Manto) de forma oblicua. Esto ocurre cuando el ángulo del plano es mayor que el de la generatriz pero menor a 90º (a < b < 90º).
-
Parábola: Surge cuando el plano de corte es exactamente paralelo a una de las generatrices del cono. Aquí, los ángulos son iguales ( a = b).
-
Hipérbola: Se genera cuando el plano corta de forma inclinada las dos hojas (o mantos) del doble cono. Para que esto suceda, el ángulo del plano debe ser menor que el de la generatriz respecto al eje (0 < b < a).
Si el plano de corte pasa por el vértice del cono, se obtienen las llamadas «cónicas degeneradas», que pueden ser un punto, una recta o un par de rectas secantes.
Pero qué tienen en común y en qué se diferencian estas curvas, veámoslo:
Una circunferencia es una línea curva cerrada y plana cuyos puntos están todos a la misma distancia (el radio) de un punto fijo llamado centro.
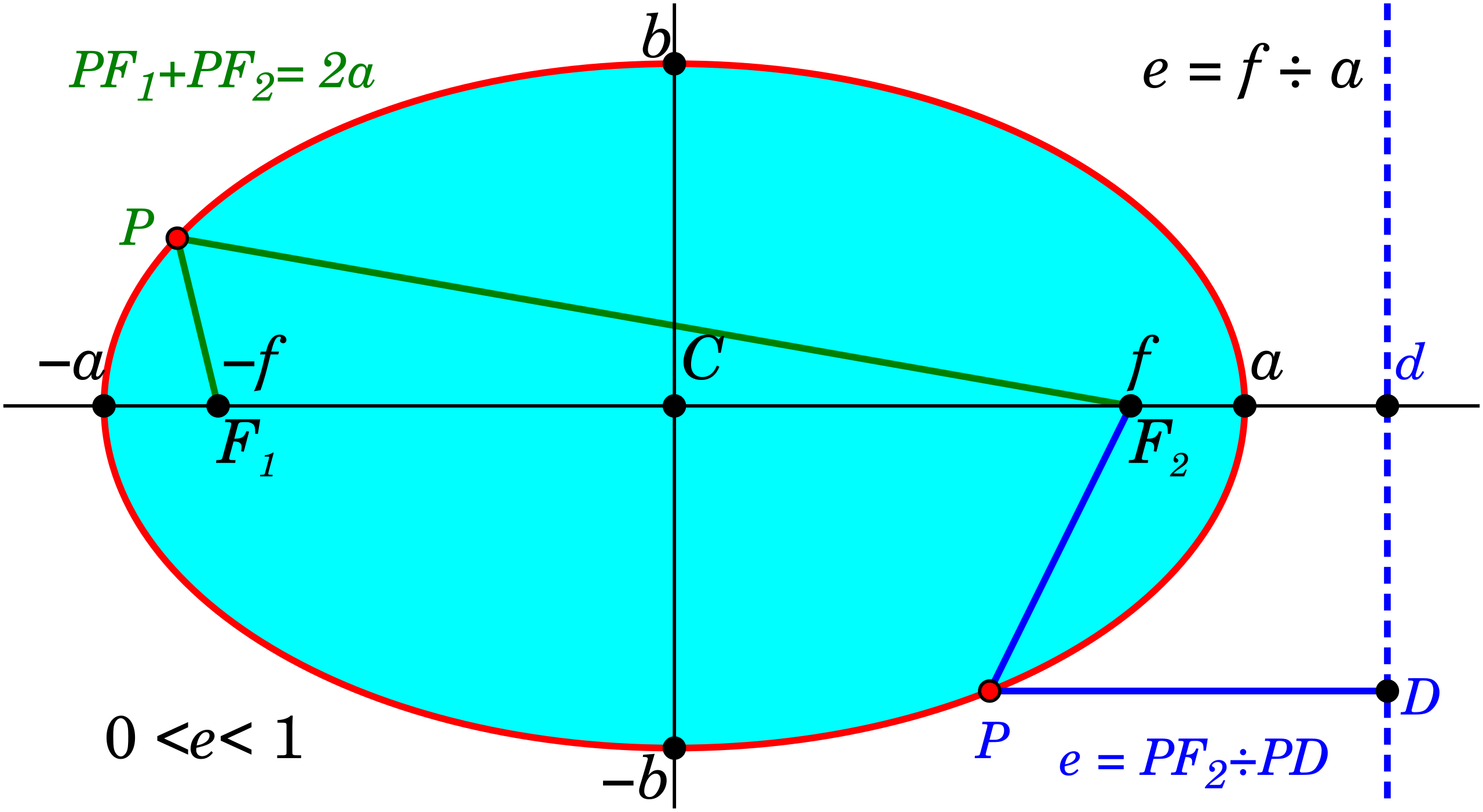
 Por su parte la elipse es una curva plana y cerrada definida como el conjunto de puntos en un plano donde la suma de las distancias a dos puntos fijos llamados focos es siempre constante. La suma de los dos segmentos verdes PF1 y PF2 es siempre la misma independientemente de donde se encuentre el punto P en la elipse.
Por su parte la elipse es una curva plana y cerrada definida como el conjunto de puntos en un plano donde la suma de las distancias a dos puntos fijos llamados focos es siempre constante. La suma de los dos segmentos verdes PF1 y PF2 es siempre la misma independientemente de donde se encuentre el punto P en la elipse.
 La parábola, por su parte, es una curva geométrica definida como el conjunto de puntos equidistantes de un punto fijo (focus) y una recta fija (Directrix).
La parábola, por su parte, es una curva geométrica definida como el conjunto de puntos equidistantes de un punto fijo (focus) y una recta fija (Directrix).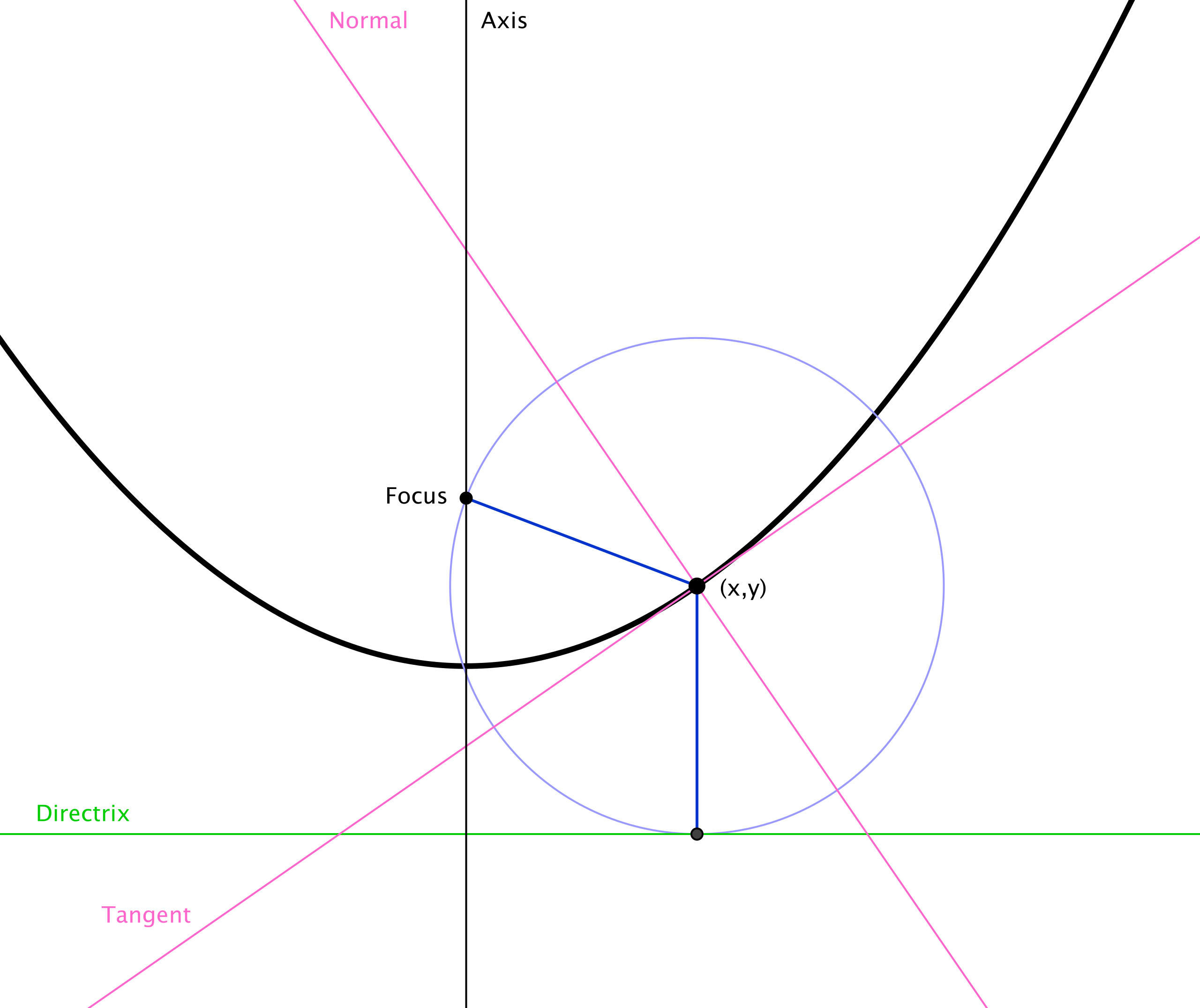
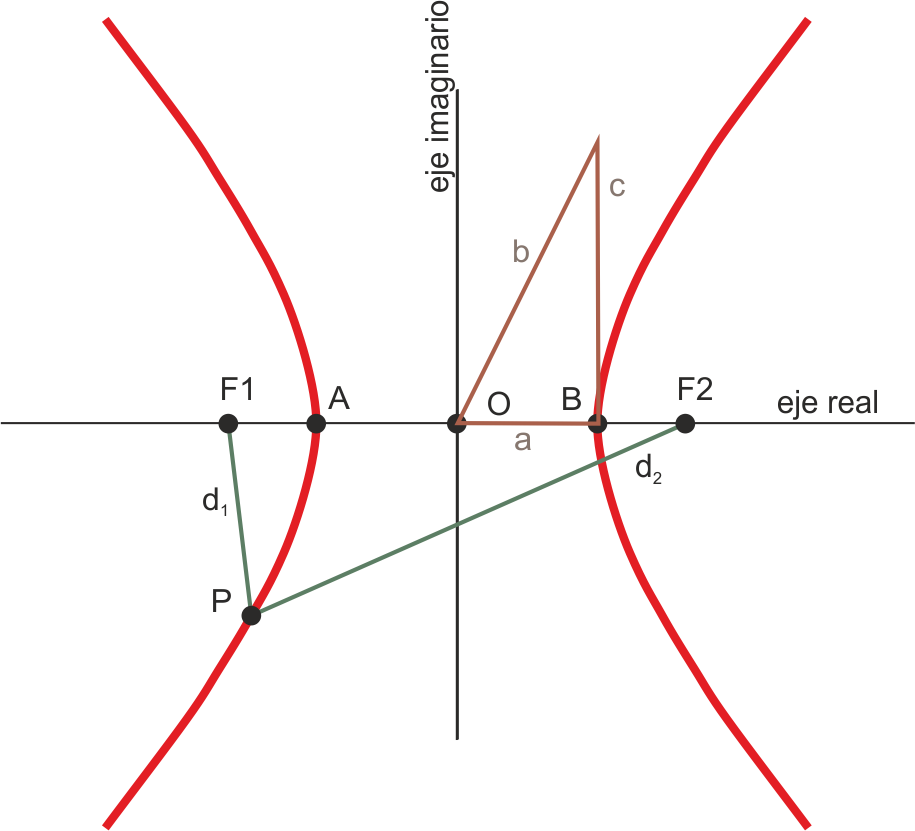
Y por último las hipérbolas se caracterizan por ser cónicas de dos ramas abiertas, definida como el lugar geométrico de puntos donde la diferencia de distancias a dos puntos fijos (focos) es constante (d2 – d1).
Y aquí voy a dejarlo porque estos han seguido tirando del hilo y podríamos estar aquí hasta la eternidad, que lo mismo con Trump y Putin por ahí no está muy lejos.
Sed buenos






















