Y tú, ¿con quién eres congruente?

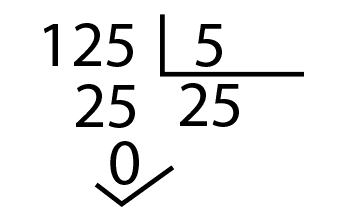
Hoy vamos a iniciar nuestro artículo con uno de los matemáticos más insignes e influyentes de la historia, Euclides (325 a. C.-ca. 265 a. C.), el cuál desarrolló su trabajo en Alejandría (antiguo Egipto), de ahí que esta ciudad vaya asociada normalmente a su nombre y conocido como “el padre de la geometría”.

Su obra más conocida son los trece libros denominados Elementos, dedicados entre otros temas al estudio y propiedades, principalmente, de figuras planas, pero también abordó conceptos como los números primos o el método de las restas sucesivas repetidas, que es lo que se denomina hoy en día como la “división euclídea”.

Acabamos de aterrizar en uno de los conceptos que hoy nos ocupa, la división euclídea o euclidiana, que este buen hombre tuvo a bien estandarizar, así que nos vamos a imaginar cómo lo hizo y de qué manera llegó a esta operación que se enseña en todos los coles. 

Situaos todos, sois mercaderes en Alejandría en tiempos de Ptolomeo I Sóter y queréis comprar trigo para posteriormente venderlo en otro lugar. El agricultor que os lo vende tiene un carro lleno con 7.540 oz (onzas) y las queréis envasar en sacas de 1000 oz para un mejor manejo. El método de las restas sucesivas repetidas consistía, en este caso, en ir llenado sacas: 

7.540 oz – 1000 oz = 6.540 oz (una saca)

6.540 oz – 1000 oz = 5.540 oz (dos sacas)

5.540 oz – 1000 oz = 4.540 oz (tres sacas)

4.540 oz – 1000 oz = 3.540 oz (cuatro sacas)

3.540 oz – 1000 oz = 2.540 oz (cinco sacas)

2.540 oz – 1000 oz = 1.540 oz (seis sacas)

1.540 oz – 1000 oz = 540 oz (siete sacas)

Sobran 540 oz

Nos llevamos siete sacas y como buenos mercaderes le decimos al agricultor que lo que sobra nos lo dé, para qué va a querer él ese regojo y además, si accede,  le vamos a pagar en ese mismo momento, listo.  

Este es el método que da pie a lo que conocemos como el Teorema de la División Euclídea que dice: para cualquier par de enteros, a (dividendo) y b (divisor), con b distinto de cero, existen enteros únicos q (cociente) y r (resto) tales que a = b·q + r, donde 0 ≤ r < |b|. Lo que conocemos de toda la vida como “el dividendo es igual al divisor por el cociente más el resto”.

En nuestro caso el dividendo son las 7.540 oz de trigo. El divisor, las 1000 oz de trigo que lleva cada saca. El cociente, las 7 sacas que hemos llenado y el resto, las 540 oz que han sobrado y que le queremos chulear al agricultor. 

Las preguntas que el mercader y el agricultor se pueden hacer son, ¿cuántas sacas se pueden llenar con el trigo que hay? (Ahí tenemos el concepto de cociente). ¿Sobrará algo de trigo? (Aquí está el concepto de resto o de división exacta, si no sobrara nada). Pues más o menos así llegaría Euclides a la noción de división euclídea, supongo…  

Como siempre, las matemáticas nacen de la necesidad o de la curiosidad humana y quizá lo difícil y la grandeza de Euclides fue abstraer la idea de la división de lo concreto.

Ahora sí estamos en condiciones de abordar el concepto de congruencia. 

Dados a y b dos números enteros y m un número natural, diremos que a y b son congruentes módulo m cuando tengan el mismo resto al dividirlos entre m, es decir, cuando a – b sea un múltiplo de m. Para resumir esta información, simplemente escribimos:

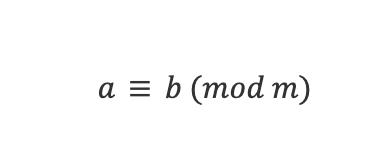
Como siempre esto se ve mejor con ejemplos.

Los números 17 y 32 son congruentes módulo 5, eso quiere decir que 17 y 32 tienen el mismo resto al dividirlos por 5 o lo que es lo mismo 32 -17 es múltiplo de 5. 

Veámoslo. 

17 = 3·5 + 2

32 = 6·5 + 2 

Los dos tienen resto 2 al dividir por 5,  o si queréis:

32 – 17 = 15 = 3 · 5  

Al restarlos es múltiplo de 5.

Como podréis comprobar el concepto de congruencia está íntimamente ligado al de la división euclídea y especialmente con el elemento resto de la misma. 

Su aplicación principal se da en el campo de la teoría de números y concretamente en estudios de divisibilidad. 

Veamos un ejemplo sencillo:

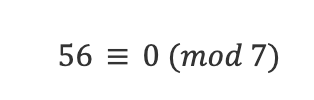
Ya que 56 = 8·7 + 0, el resto al dividir 56 entre 7 es 0, la división es exacta y en ese caso decimos que 56 es múltiplo o divisible por 7.

Lo interesante de las congruencias es que cumplen unas propiedades muy majas, las dos más significativas, que no vamos a demostrar, son estas: 

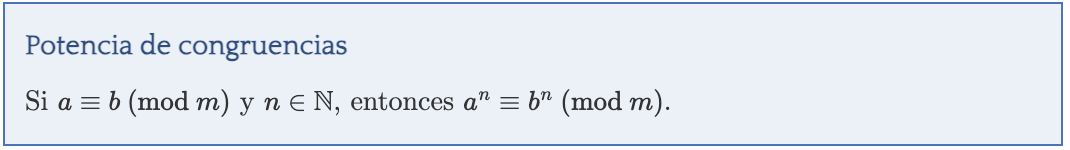
A partir de ellas os voy a poner un ejemplo ya más complejo del potencial que tienen las congruencias. 

Supongo que vuestro primer intento será meterlo en la calculadora, pero no os molestéis porque no es capaz de procesarlo, ni la del móvil. 

Aplicando congruencias:

Entonces

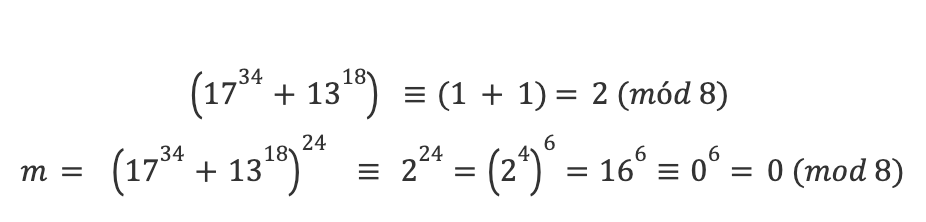
Por lo que podemos concluir que m es múltiplo de 8.

Si os habéis perdido, da igual, por congruencias hemos llegado a que números que ni siguiera los ordenadores más potentes del mundo son capaces de procesar podemos deducir si son divisibles o no por otros. 

Bienvenidos al mundo de las congruencias, es un campo muy potente y con muchas aplicaciones, es una herramienta fundamental de la aritmética que permite simplificar cálculos y resolver problemas de divisibilidad, de sistemas de ecuaciones diofánticas y son clave en la criptografía moderna para proteger información (como en el sistema RSA); además, se aplican en la verificación de códigos (ISBN, tarjetas de crédito) y en cálculos cotidianos como los calendarios y los relojes, mostrando su importancia tanto en la teoría de números como en la vida diaria.

Termino dedicando este artículo a las personas con las que me ha tocado compartir este último mes en el proceso selectivo de personal docente en Extremadura como tribunales por la especialidad de matemáticas, espero que cada uno de ellos haya sentido congruencia mód 5 con sus compañeros, deseo que cada miembro de la comisión de selección haya experimentado esa misma congruencia dentro de ella y entre todos hayamos podido ser congruentes mód 30. 

A los aspirantes que lo consiguieron, enhorabuena y a los que se quedaron en el camino, paciencia y constancia, al final llega, os lo digo por experiencia. 

Sed buenos